by Maths Town
Watercolor on Perpendicular Julia
IPFS

19 December 2021•TEZOS•IPFS
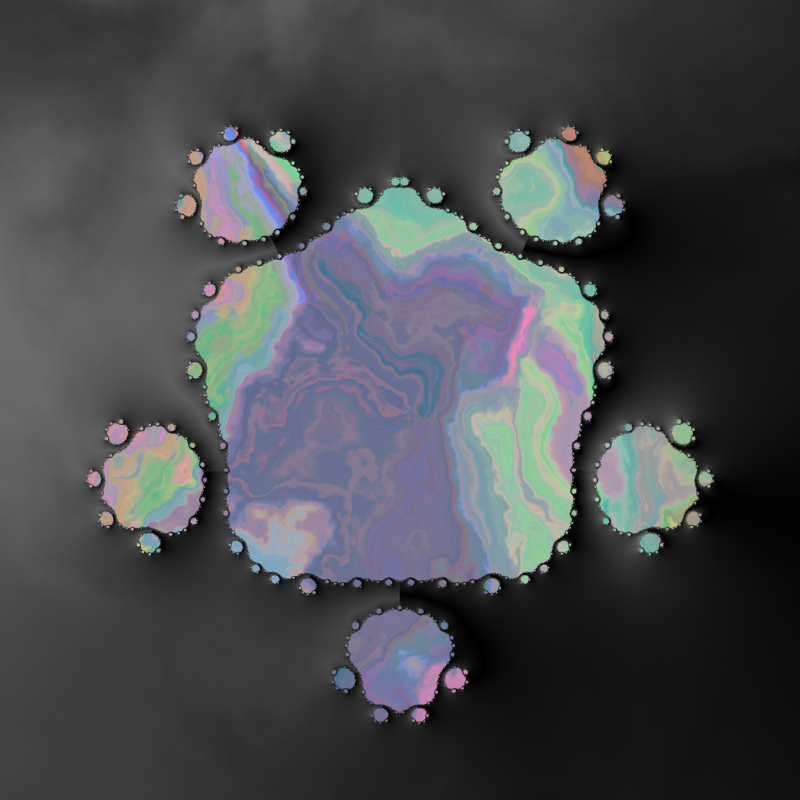
“Watercolor on Perpendicular Julia” is a follow-up the original “Watercolour on Julia”. It features my personal favorite fractal, the Perpendicular Mandelbrot. The Julia Sets of this fractal are very interesting because of their symmetry. They are symmetrical from left to right. Interestingly, these folds are also found in the sub structure of each shape. This non-analytic structure ensures there are a huge range of possible shapes.
Unlike normal Julia Sets it is possible that the Perpendicular Julia sets could be filled with holes. Some of the most interesting shapes of this algorithm will only appear rarely.
Another fun feature of the symmetry is that some of shapes will occasionally resemble creatures or faces. If you get one of these, consider yourself lucky. (If you feel the urge to draw eyes onto him, be sure to tag me on Twitter.) 😊
Unlike normal Julia Sets it is possible that the Perpendicular Julia sets could be filled with holes. Some of the most interesting shapes of this algorithm will only appear rarely.
Another fun feature of the symmetry is that some of shapes will occasionally resemble creatures or faces. If you get one of these, consider yourself lucky. (If you feel the urge to draw eyes onto him, be sure to tag me on Twitter.) 😊
Fractal Art by Maths Town
I operate the "Maths Town" channel on YouTube. https://www.youtube.com/c/mathstown
mathstown.tez
mathstown.eth
46 EDITIONS
•0 RESERVES
minted
46 / 46
fixed price
1 TEZ
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH