by dirx
Still C
IPFS

10 May 2025•BASE•IPFS
Just a big dot with a lot of little dots inside.
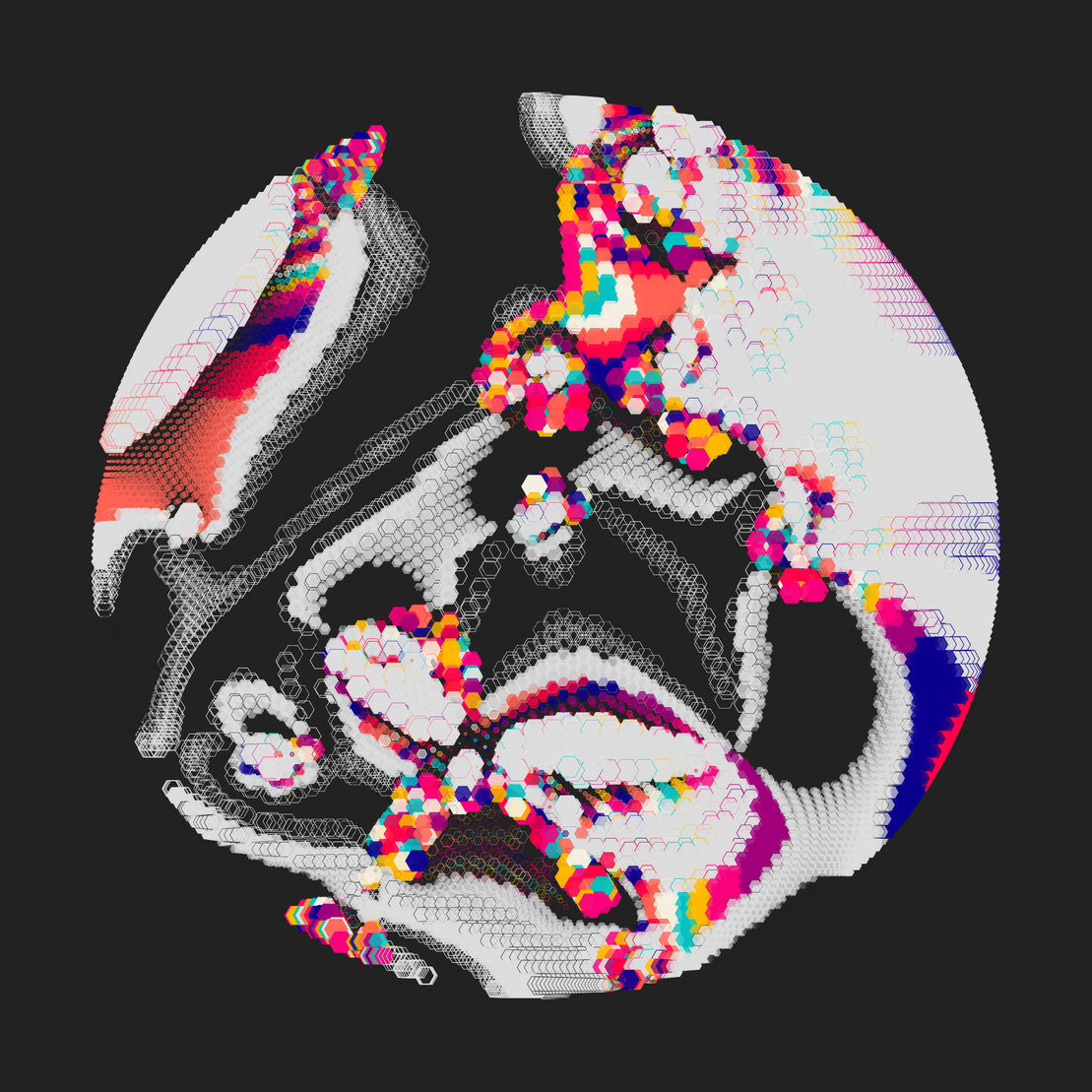
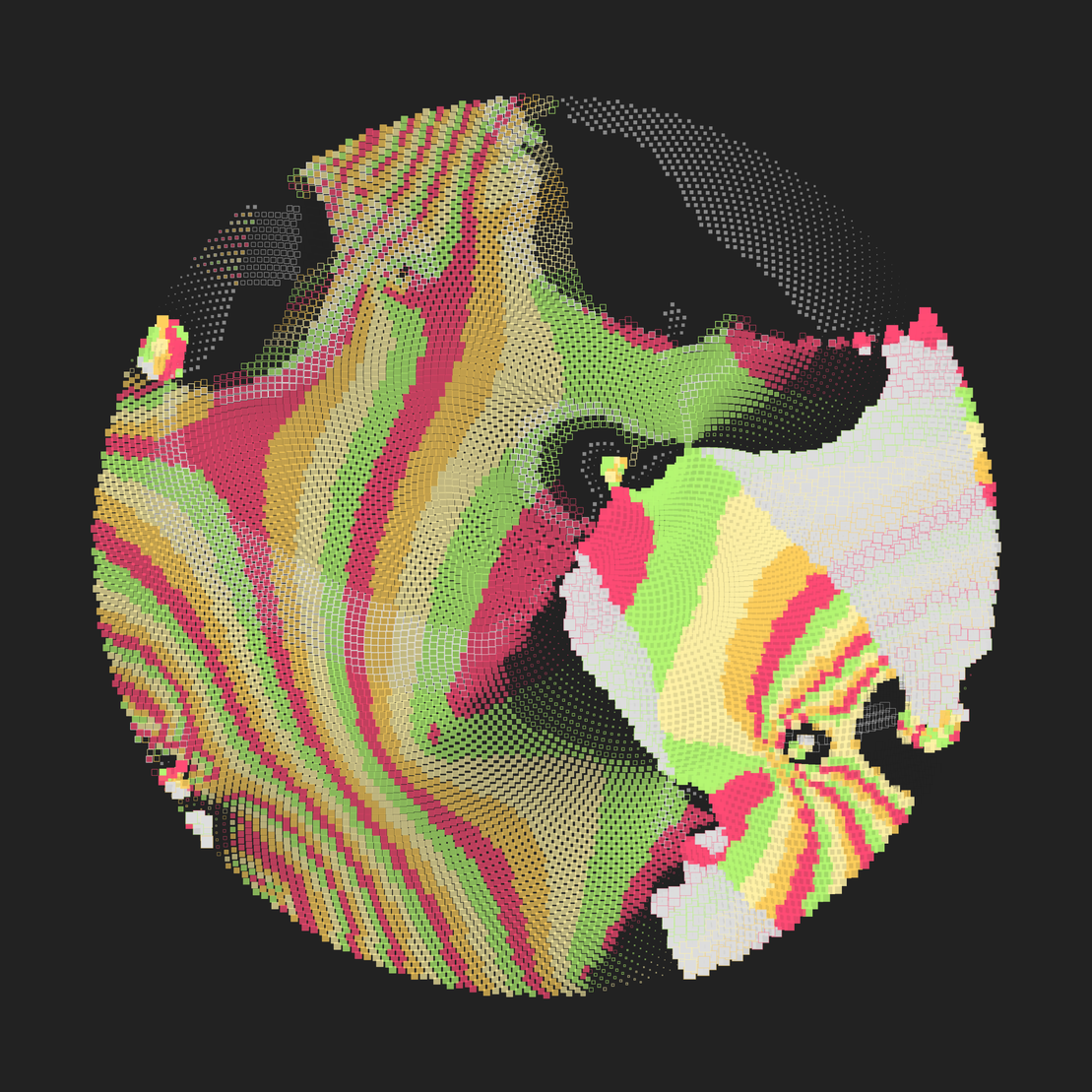
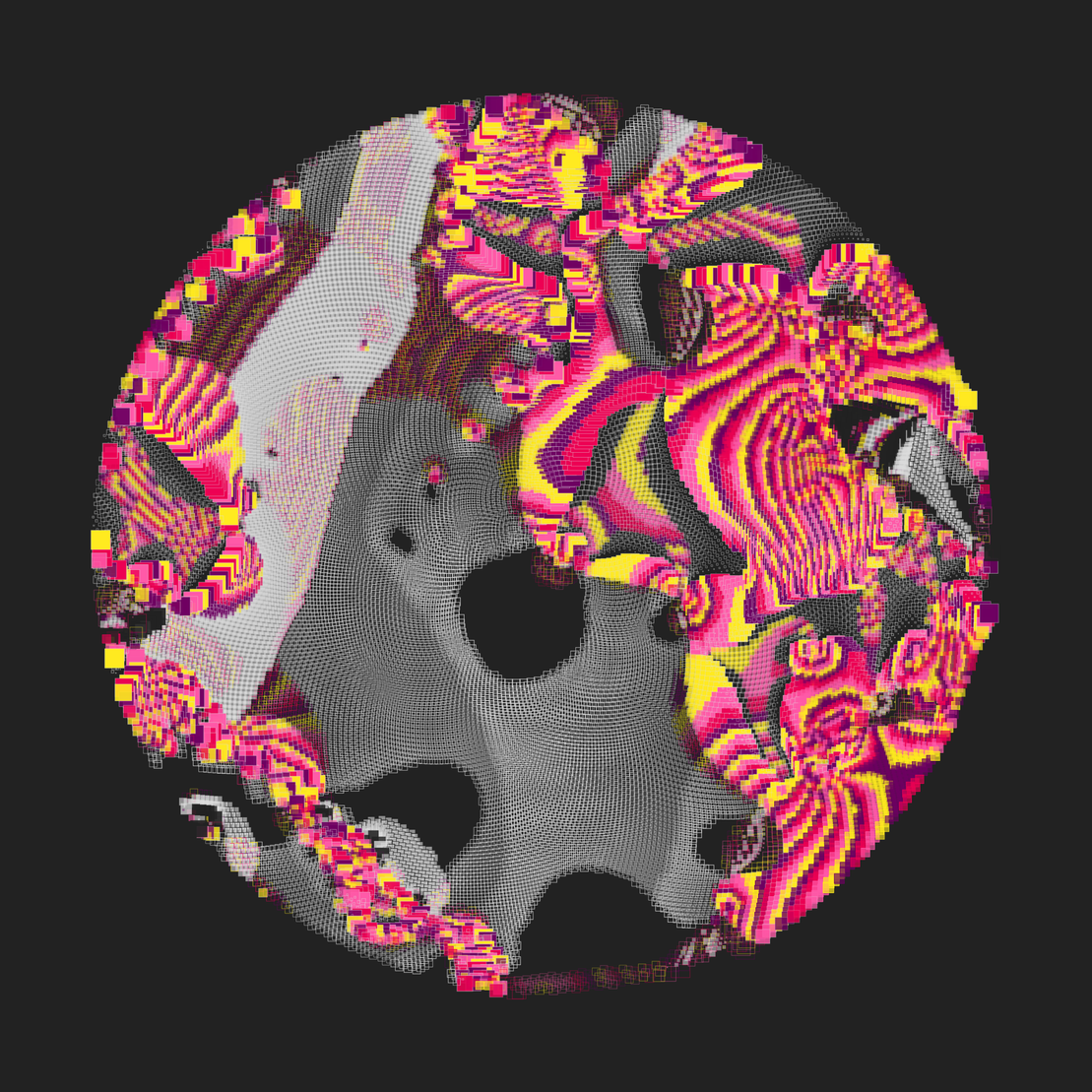
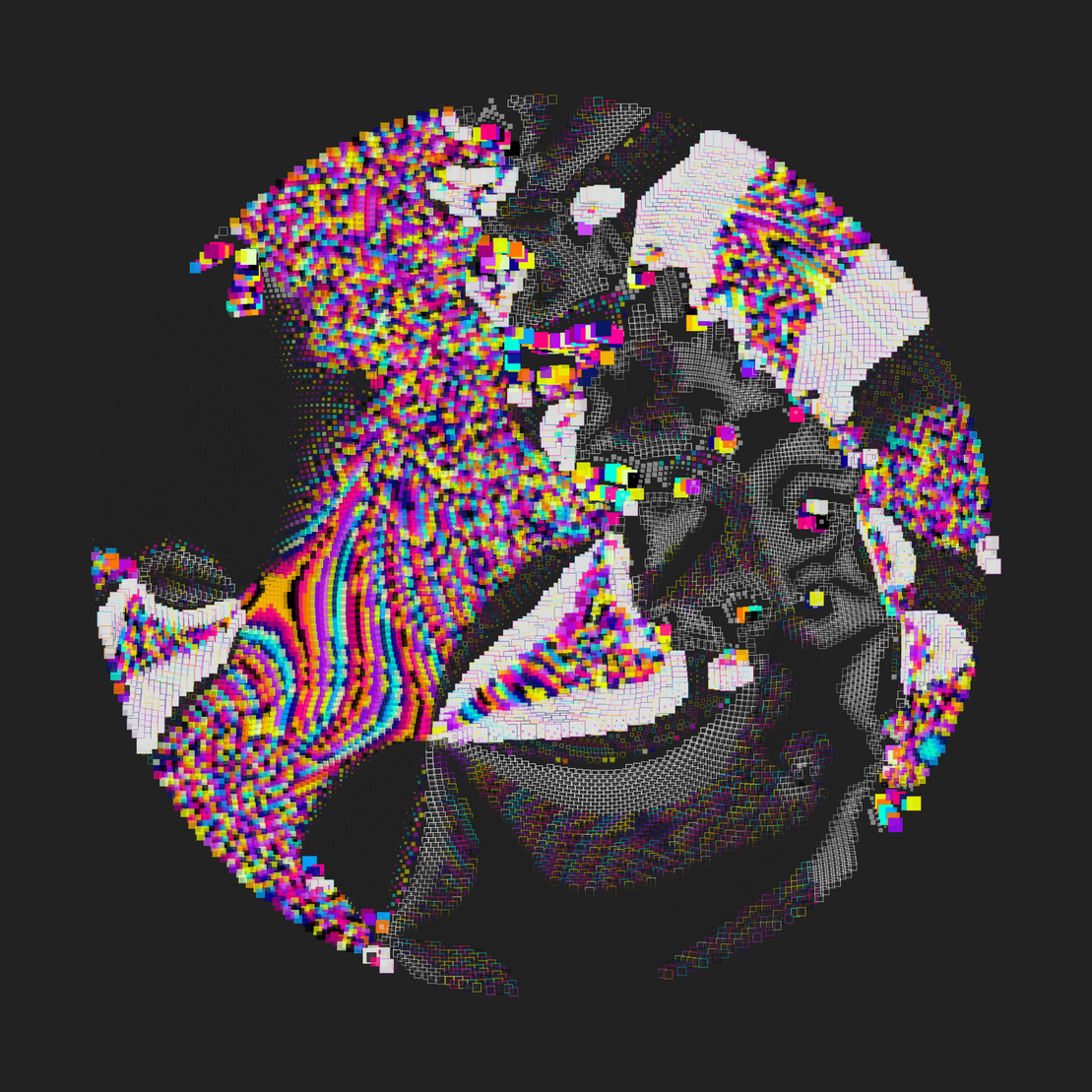
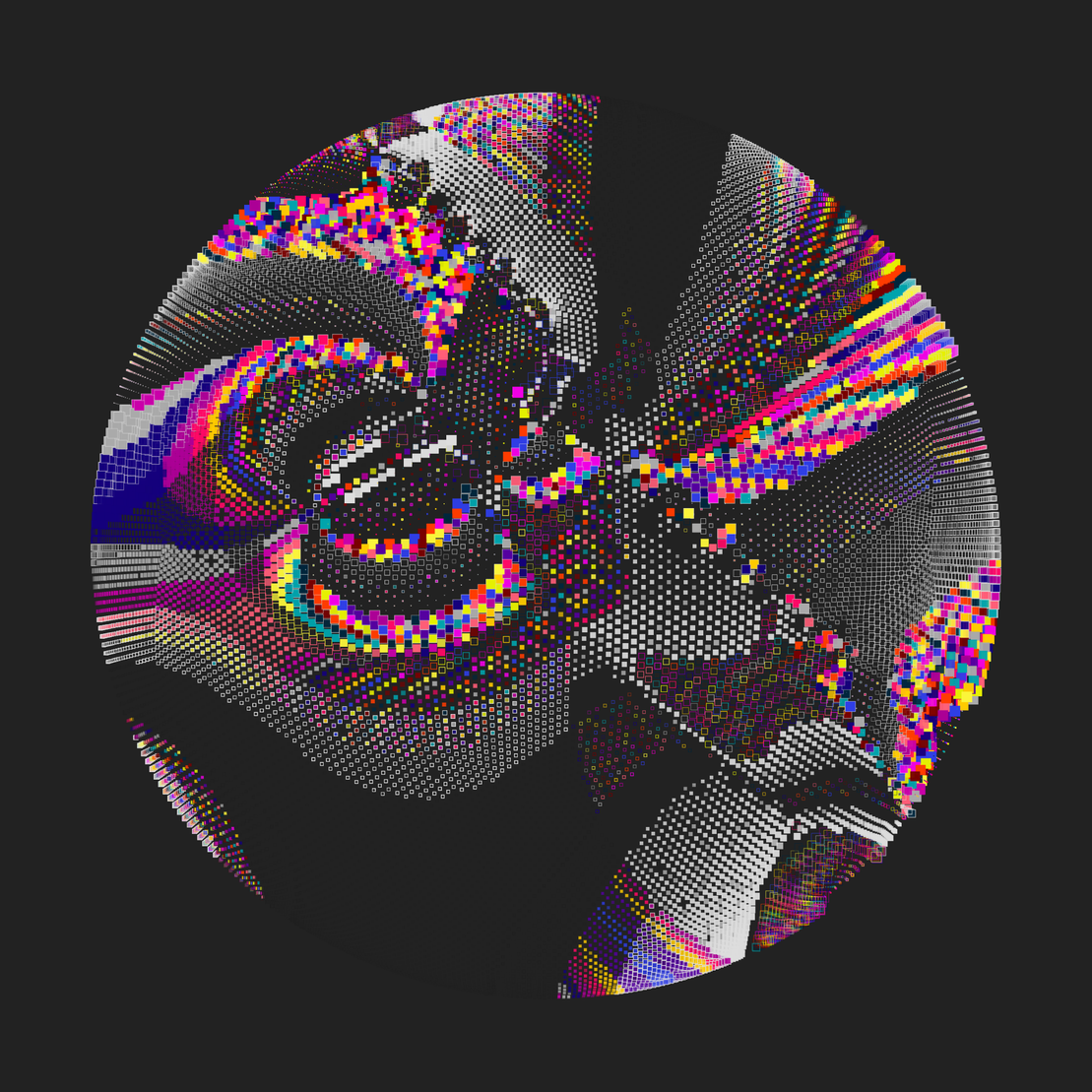
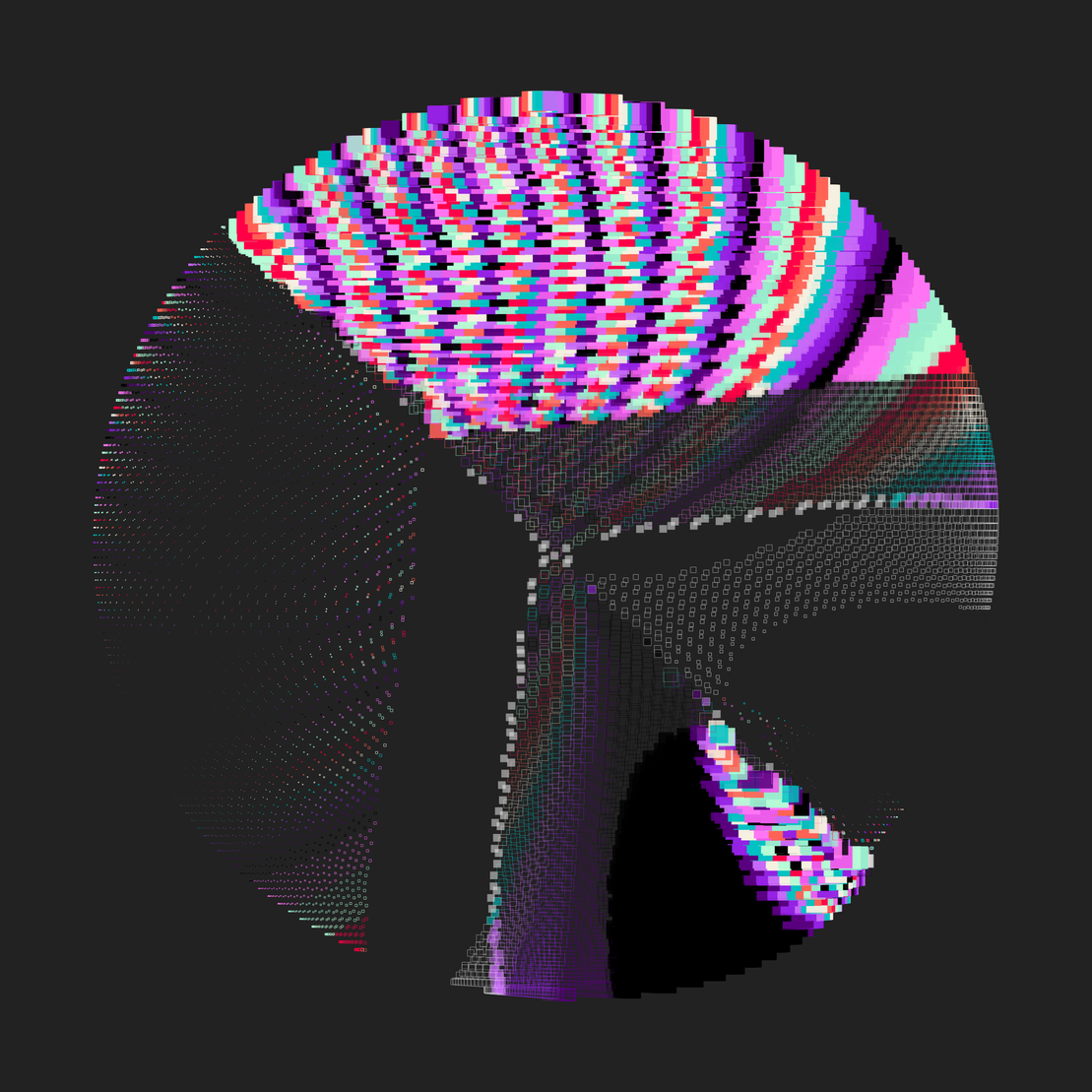
This piece arranges shapes with varied fill patterns and outlines, leveraging transformer and traversal algorithms while responding to an underlying flow field system.
Features:
- dotSize (2-7) - base size of each shape
- gridSize (98-175, step: 7) - grid resolution
- palettes (1-4) - number of random 4-color palettes
- attractors (21-175, step: 7) - flow field influence points
- attractorStrength - attractor influence function (linear, sine, sineSquared, easeIn, smoothstep, parabola, sigmoid)
- x - horizontal coordinate transformation function (linear, sine, sineSquared, easeIn, smoothstep, parabola, sigmoid)
- y - vertical coordinate transformation function (linear, sine, sineSquared, easeIn, smoothstep, parabola, sigmoid)
- distributor - point distribution algorithm (fermatsSpiral, fibonacciLattice, sphericalSpiral, geodesicSphere)
- traverser - traversal algorithm (row, column, zigZagRow, zigZagColumn, diagonal, bfs, dfs, random)
- kick - position/color adjustment function (linear, sine, sineSquared, easeIn, smoothstep, parabola, sigmoid)
- repeat (1-25) - color pattern frequency
- fills - shape fill strategy (more or less of palette colors, light, dark or no fill)
- strokes - shape outline strategy (more or less of palette colors, light, dark or no outline)
- shape - quad, hexagon or circle
Shortcuts & interactions:
- `h` to toggle help
- `p` to download as png
- `s` to download as svg
This piece arranges shapes with varied fill patterns and outlines, leveraging transformer and traversal algorithms while responding to an underlying flow field system.
Features:
- dotSize (2-7) - base size of each shape
- gridSize (98-175, step: 7) - grid resolution
- palettes (1-4) - number of random 4-color palettes
- attractors (21-175, step: 7) - flow field influence points
- attractorStrength - attractor influence function (linear, sine, sineSquared, easeIn, smoothstep, parabola, sigmoid)
- x - horizontal coordinate transformation function (linear, sine, sineSquared, easeIn, smoothstep, parabola, sigmoid)
- y - vertical coordinate transformation function (linear, sine, sineSquared, easeIn, smoothstep, parabola, sigmoid)
- distributor - point distribution algorithm (fermatsSpiral, fibonacciLattice, sphericalSpiral, geodesicSphere)
- traverser - traversal algorithm (row, column, zigZagRow, zigZagColumn, diagonal, bfs, dfs, random)
- kick - position/color adjustment function (linear, sine, sineSquared, easeIn, smoothstep, parabola, sigmoid)
- repeat (1-25) - color pattern frequency
- fills - shape fill strategy (more or less of palette colors, light, dark or no fill)
- strokes - shape outline strategy (more or less of palette colors, light, dark or no outline)
- shape - quad, hexagon or circle
Shortcuts & interactions:
- `h` to toggle help
- `p` to download as png
- `s` to download as svg
OPEN EDITIONS UNTIL June 18, 2025 @ 18:00
minted
43540
fixed price
0 ETH (Base)
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH