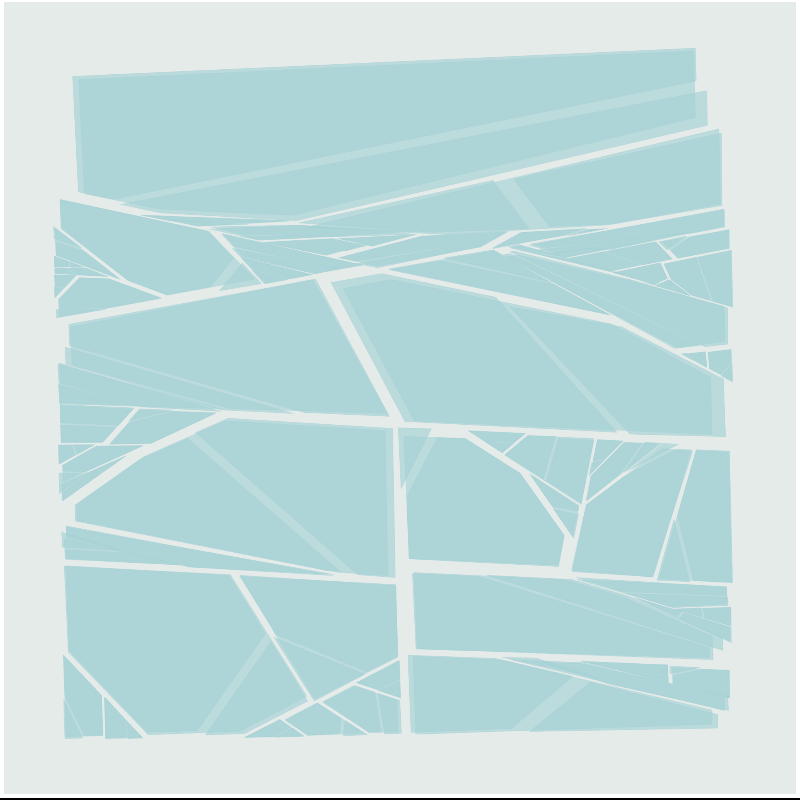
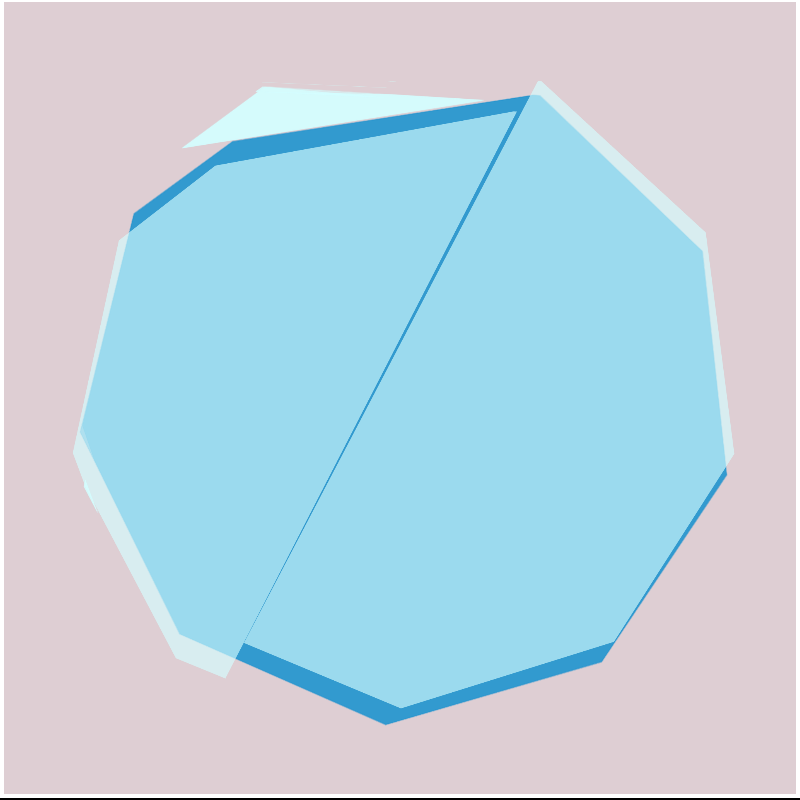
‘Shattered’ offers sad reminders of dropped phones, that broken Game Boy and the Apple Watch you thought you'd placed carefully on the side of the sink, only to watch fall in irrevocable slow-motion to the tiled floor beneath.

Crunch.

Beginning with a perfect, unbroken pane of polygonal glass, ‘Shattered’ repeatedly bisects, creating ever smaller parts by selecting two sides and creating splintered shards along that axis. Equal breaks are possible—the creation of two symmetrical fragments—but mostly uninteresting, so a weighting factor is applied that leads to uneven, splintered pieces and tiny broken fragments. The beginning and end points of the fractures are slightly more likely to be near the corners.

For variety, the starting polygon may be a simple rectangle, perhaps pre-emptively cracked into two parts to give the algorithm a gentle, shaping nudge; possibly instead the piece will begin with a pair of crossed polygons, or a regular polygon; perhaps even a myriad-sided polygon with aspirations of circularity. Occasionally, a hole is built into the shape, a complex mathematical undertaking but one well worth the calculations, splitting the starting point into shards as though from an impact or sharp blow.

Numerous colour palettes are possible; these are curated rather than randomly-generated, although the intensity and structure of the colours within the palette are subject to the whims of shaped random functions.

A further source of variation lies within the shattering algorithm itself: as the iterations increase the algorithm produces progressively splintered pieces, ranging from an elegant three or four cracks to the shattered desolation of a MacBook that's been dragged off the coffee table by its power cord. The mathematics is paradoxically both simple and complex, since all that's necessary is to iterate over an array of points, identifying opposites and generating new points that lie between them. As with the splintered fragments of a broken pane of glass, the devil is in the sharp-edged details.

I should note that the variance offered by the chosen palettes allow for extremes of low contrast, all part of allowing suitable variation. In testing I find these blank-looking pieces to be exquisitely rare, but possibly unwelcome: I will happily buy back any piece you find ‘unpalatable’ for the minting price of 1 tez, with that pun there thrown in for free. Find me on Twitter.