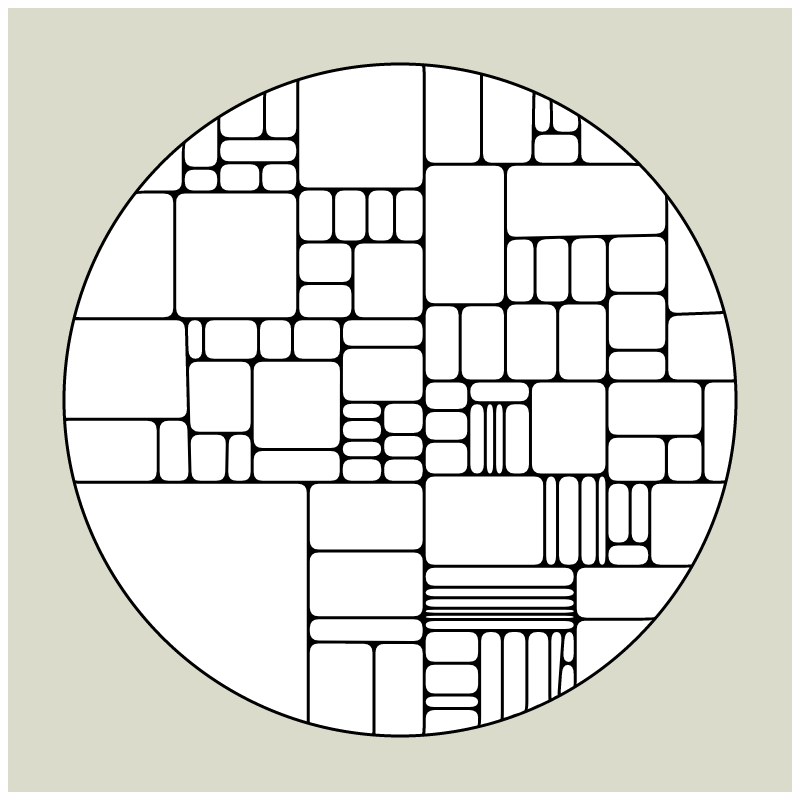
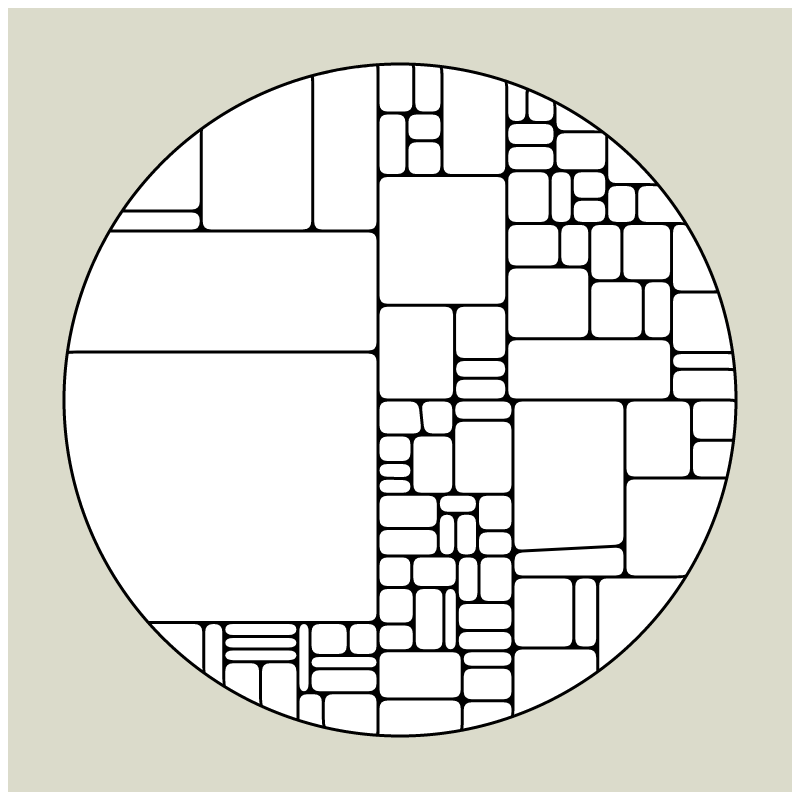
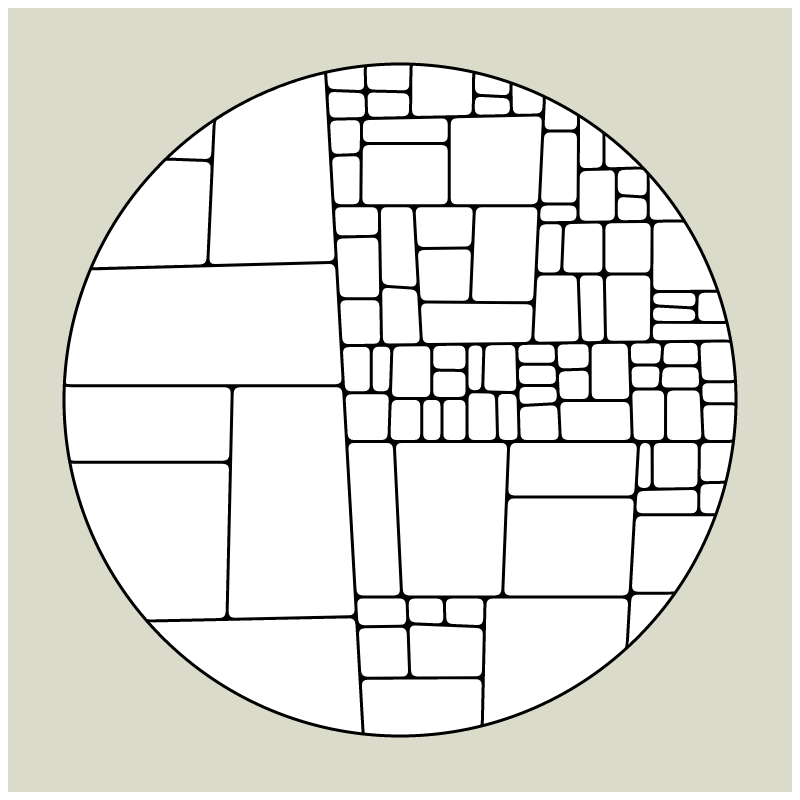
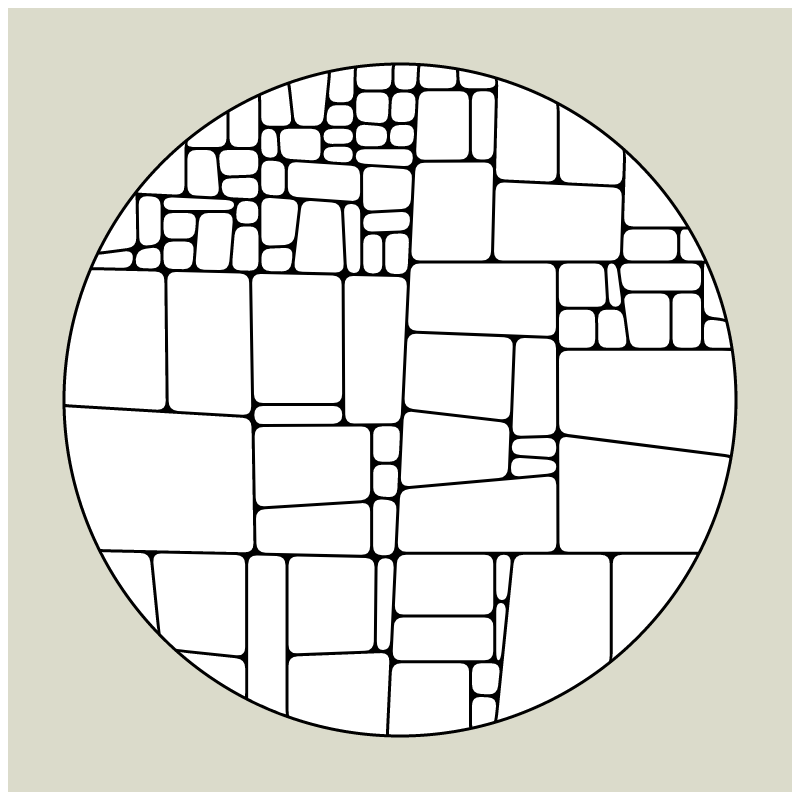
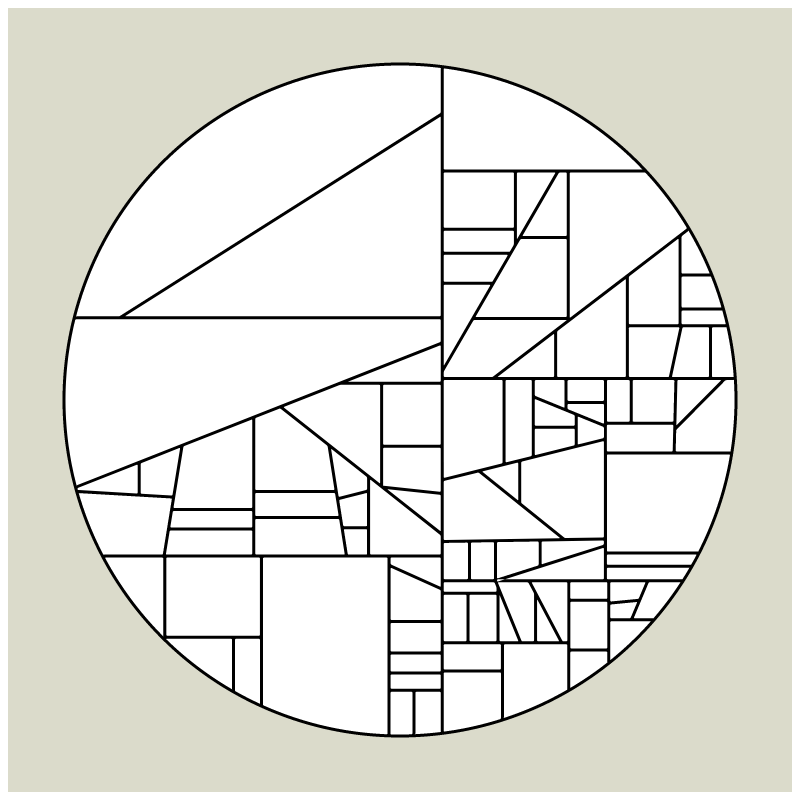
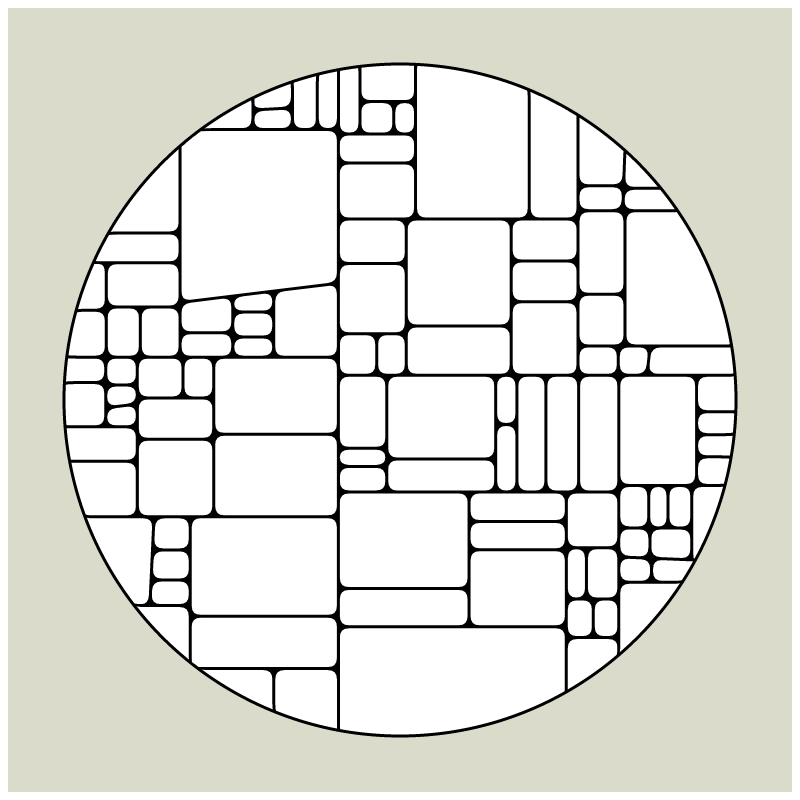
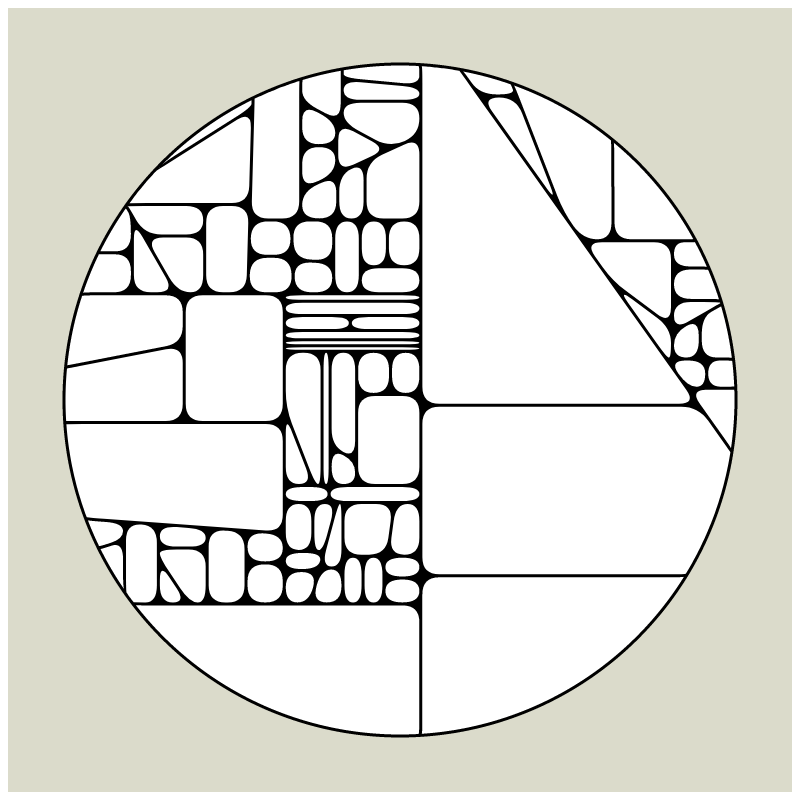
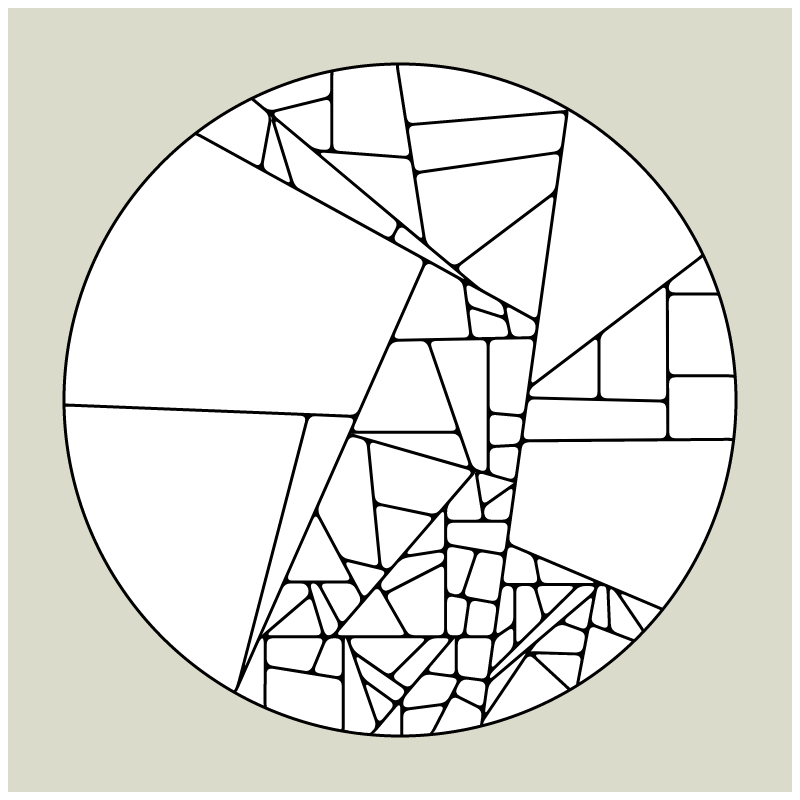
My first mint on fx(hash) together with HEK - Haus der elektronischen Künste, is a revisit of my early explorations of computational geometry which I had started in 2008 when my tool of choice was still Flash and ActionScript. Since Flash does not exist anymore most of what I had created over a course of 12 years is almost impossible to view in its original form these days and large parts of my beginnings in generative art are lost in time now.

In these early experiments I started building my personal generative library QuasimondoLibs which consisted of a ever growing set of algorithms for geometry and pixel manipulation. Over the years I had ported most my library to Javascript and Python and this work uses the JS version of it.

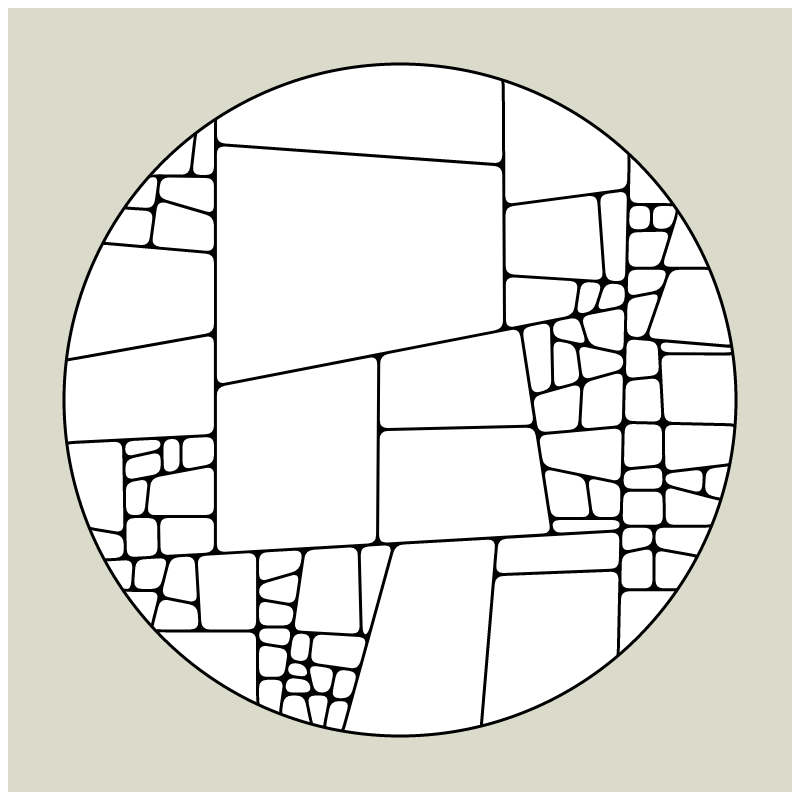
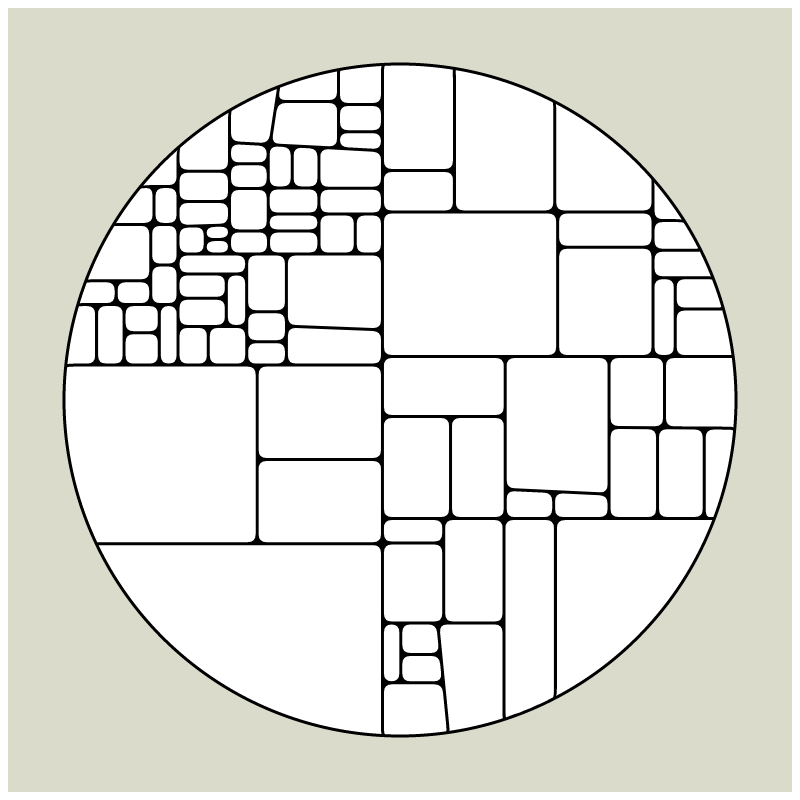
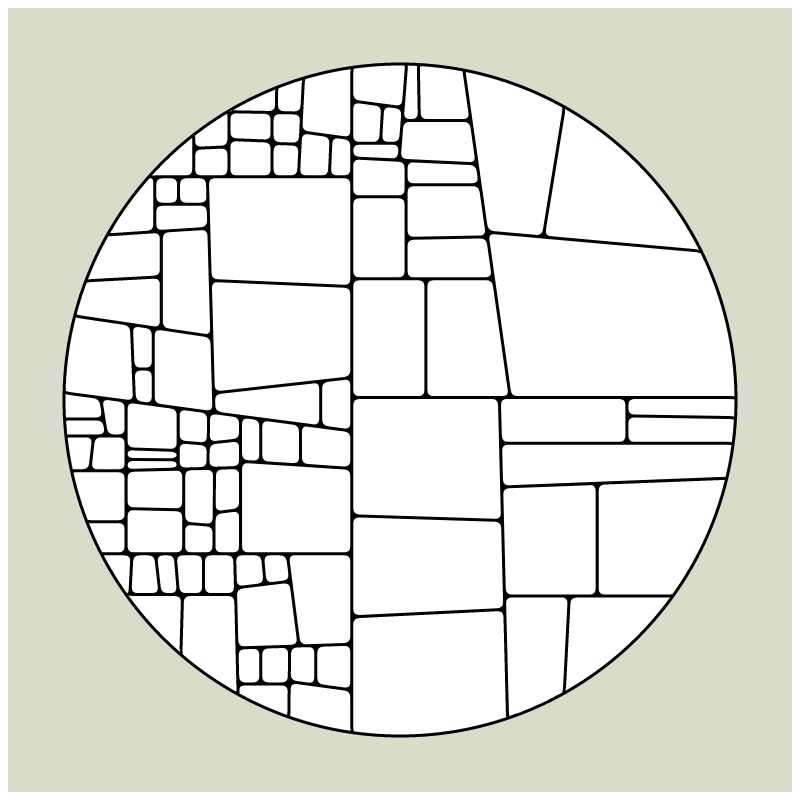
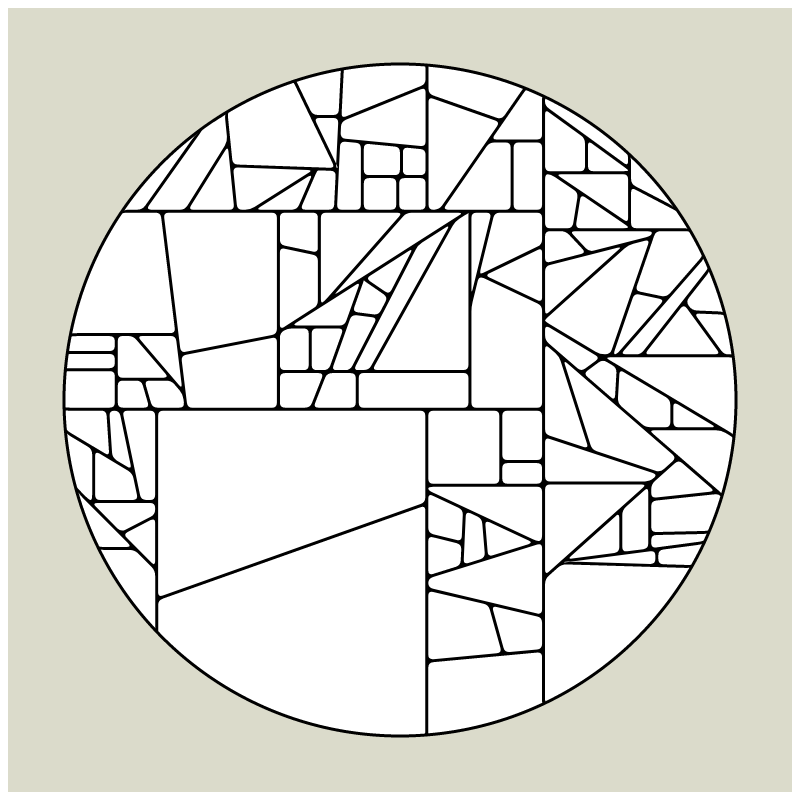
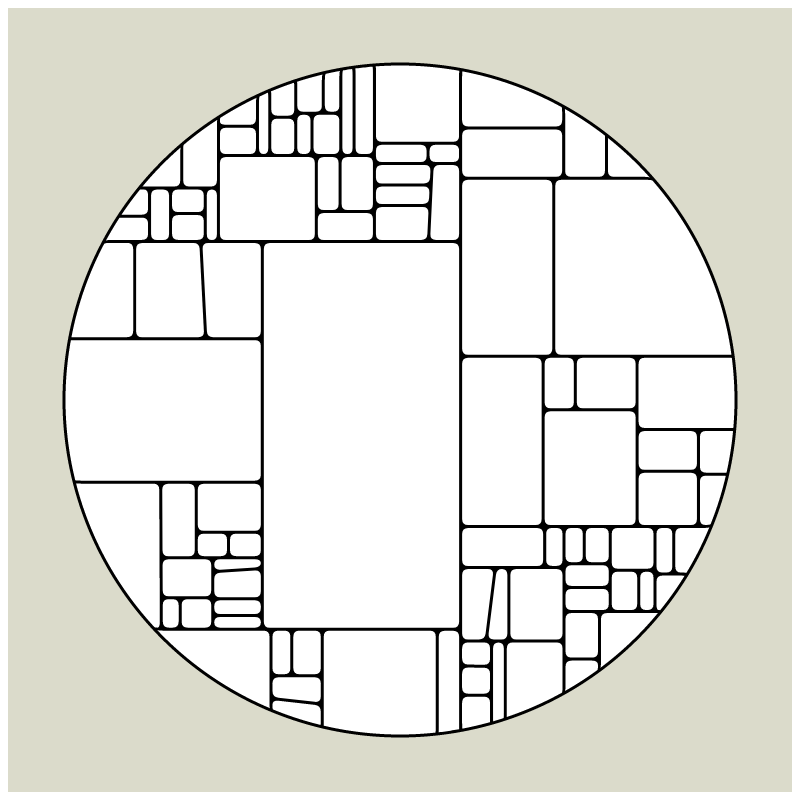
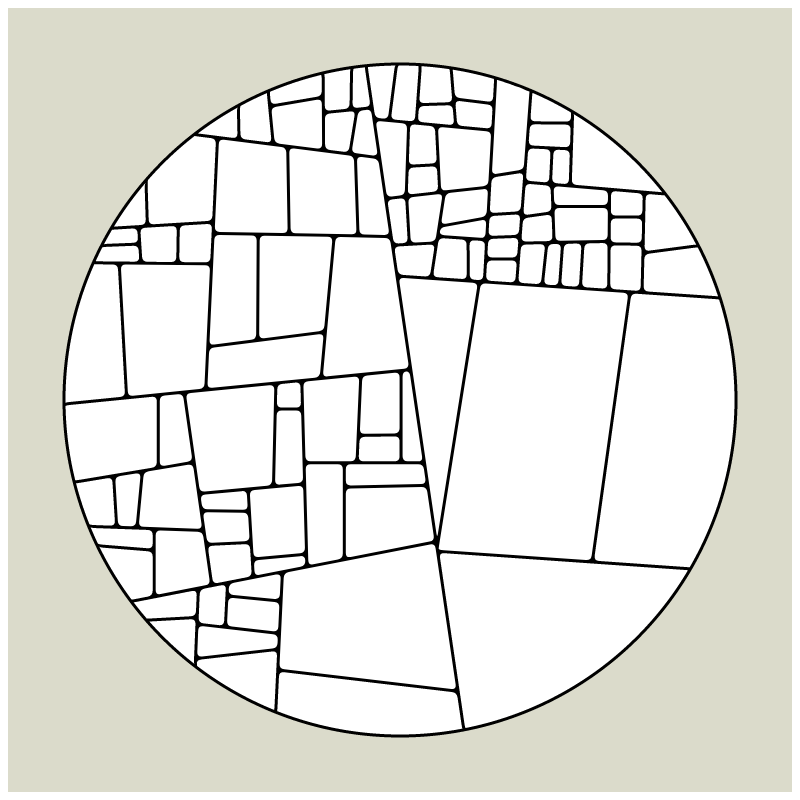
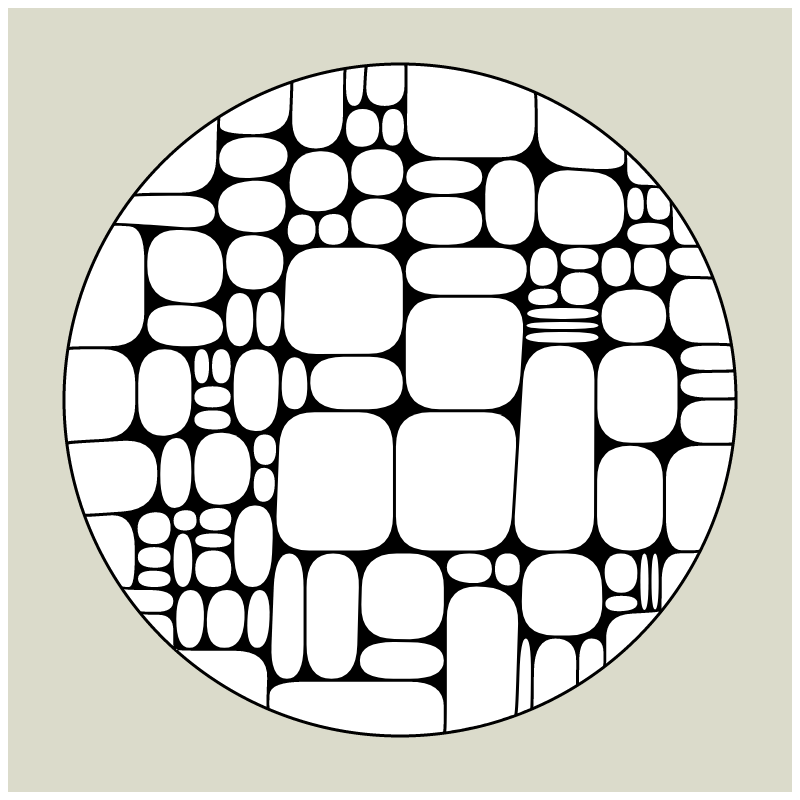
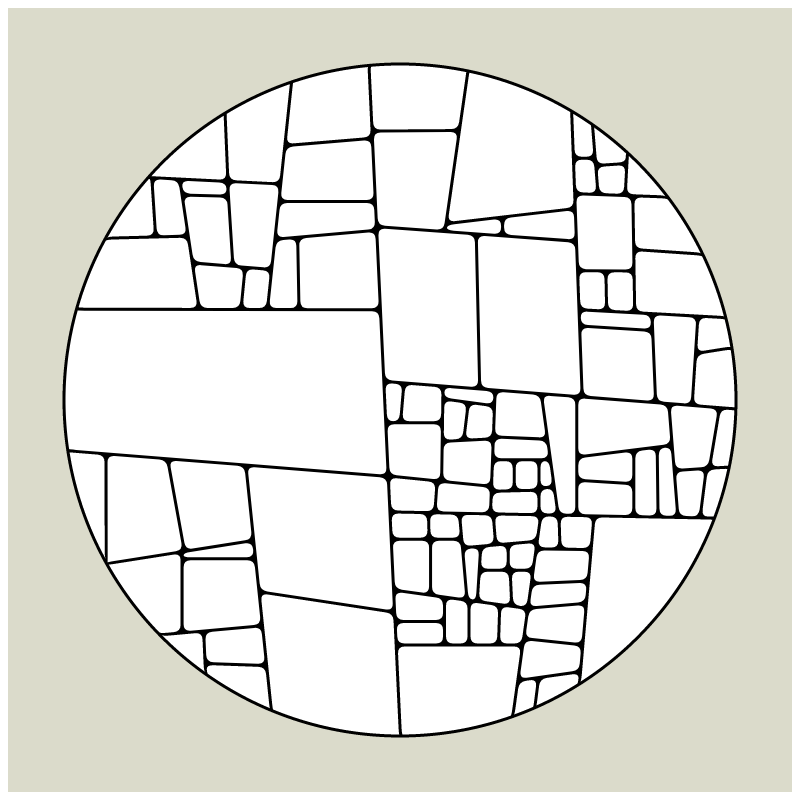
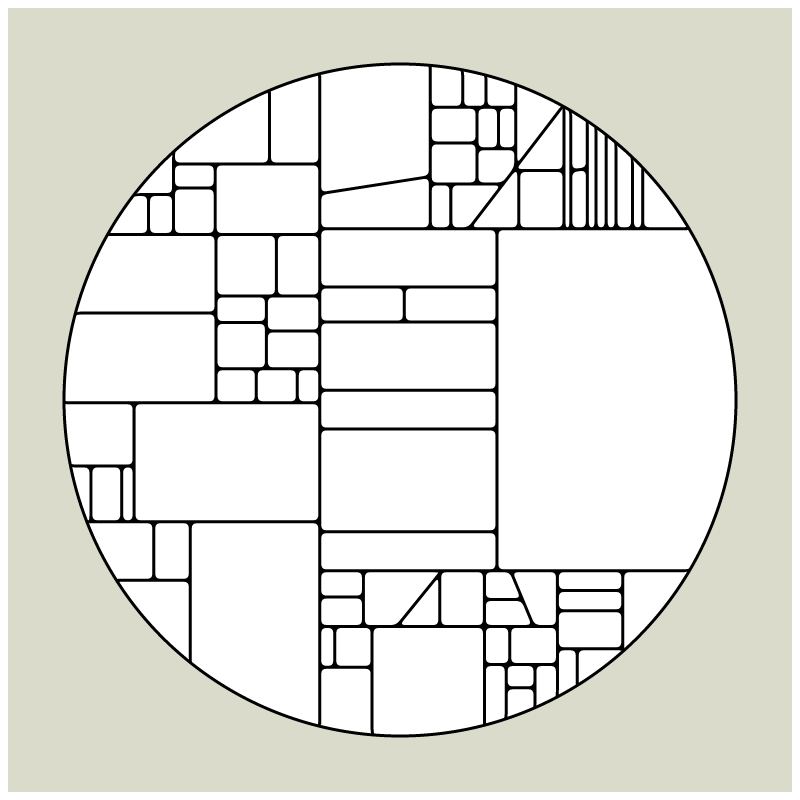
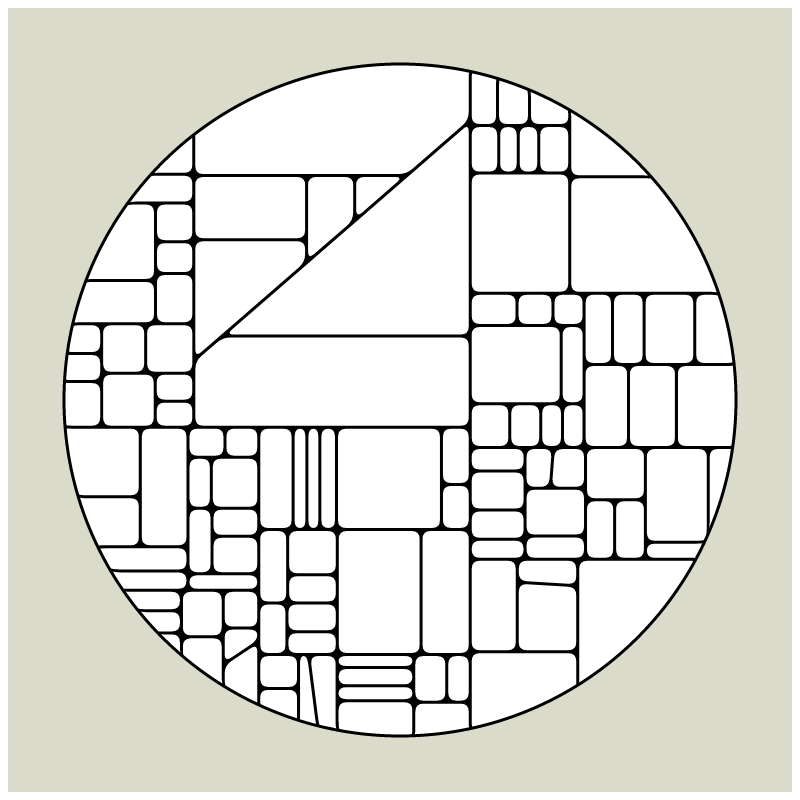
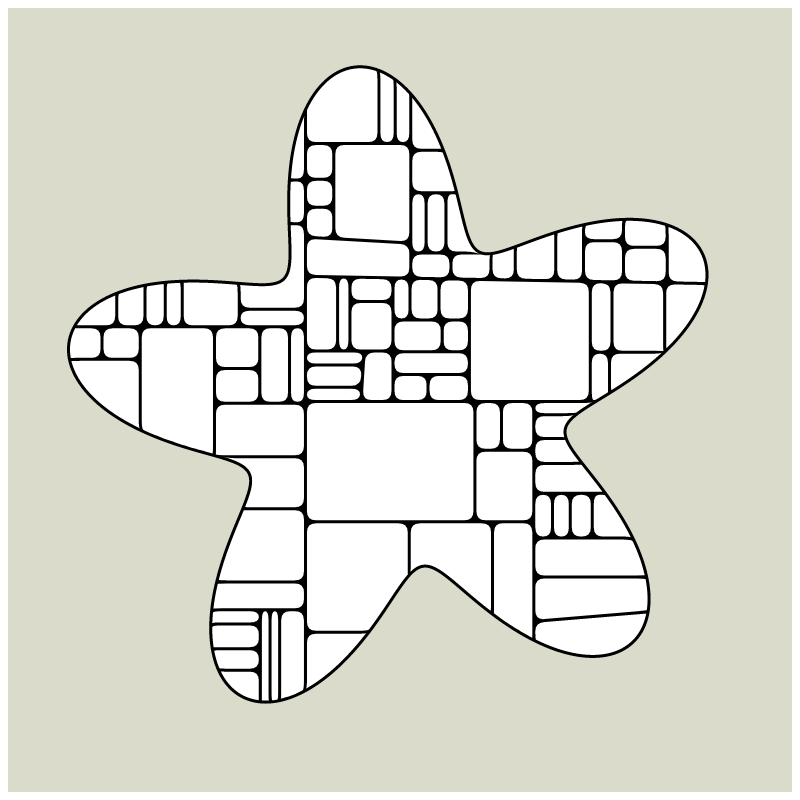
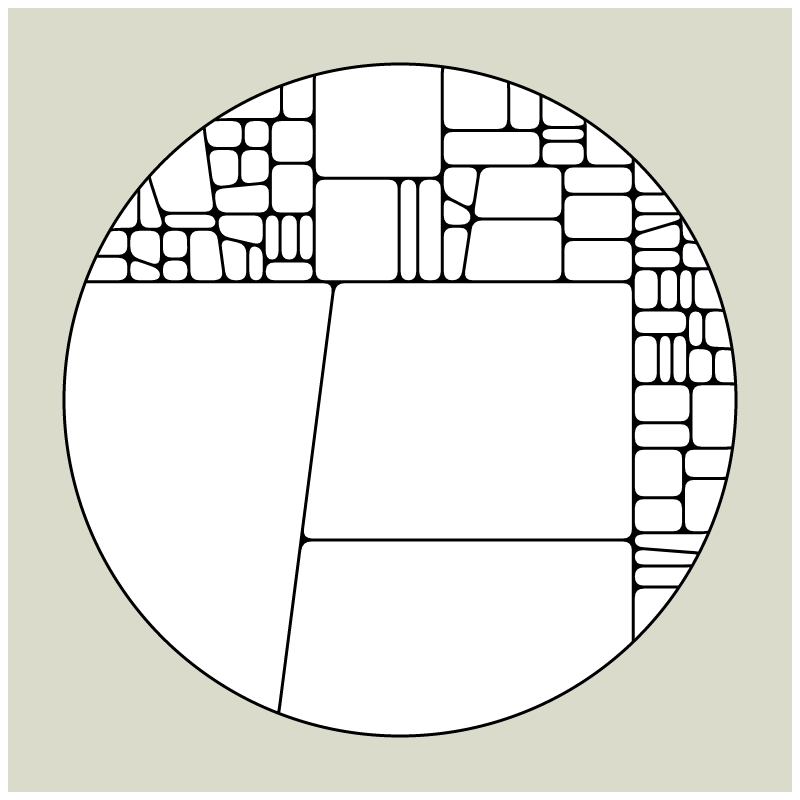
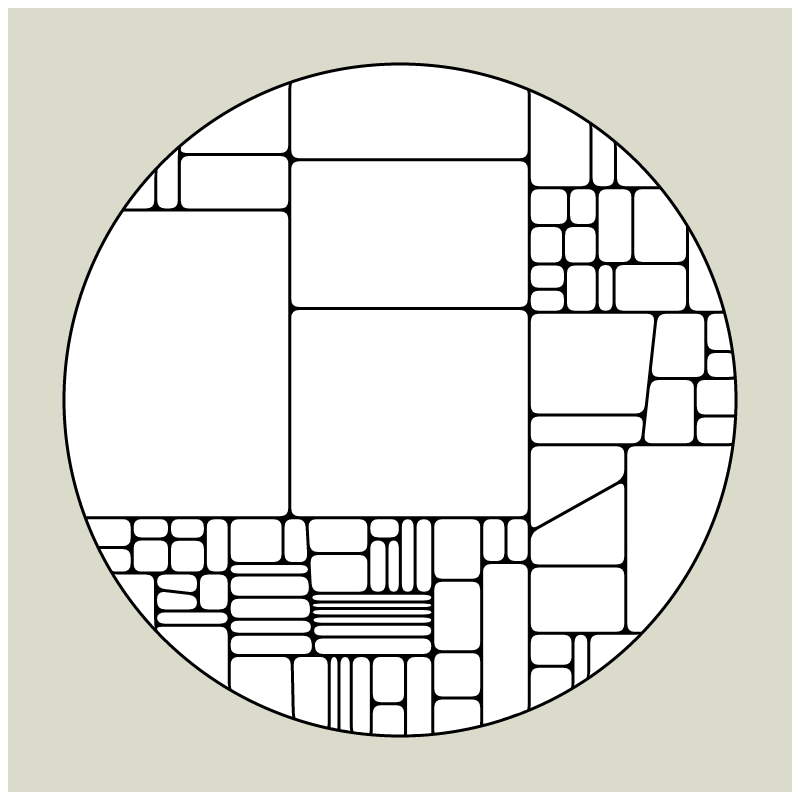
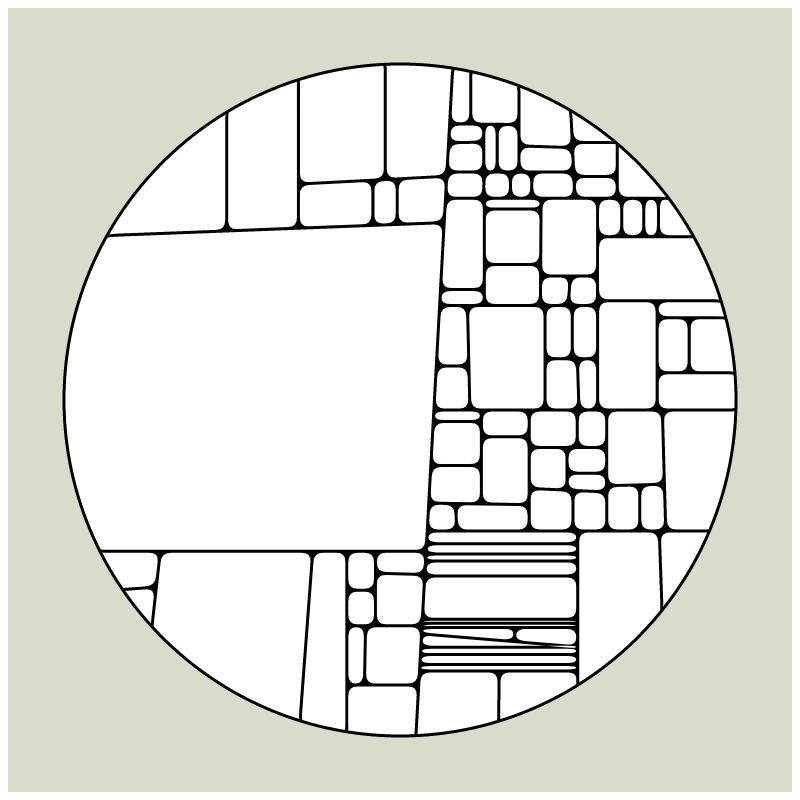
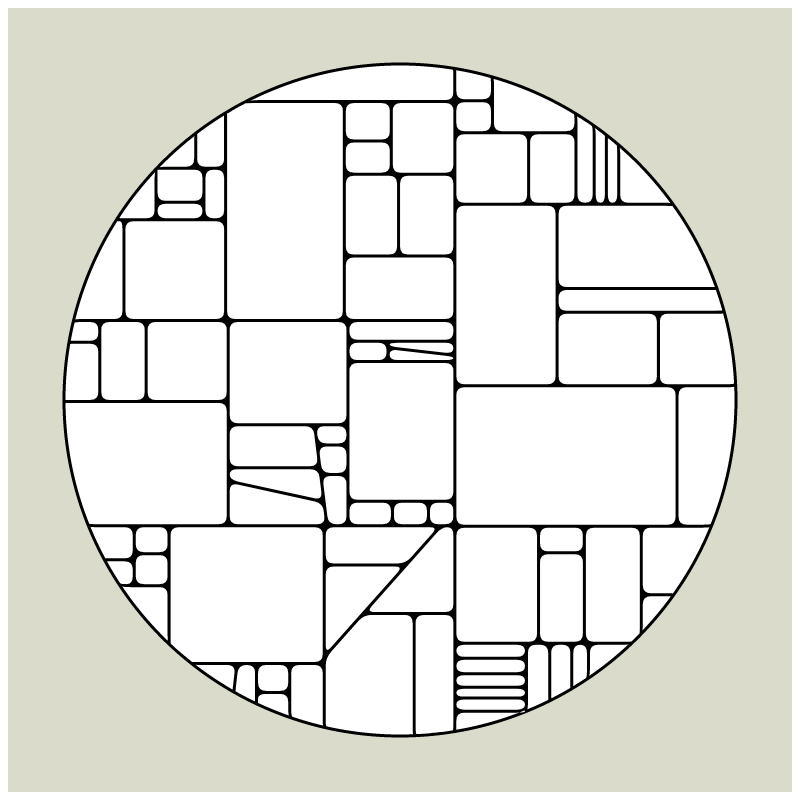
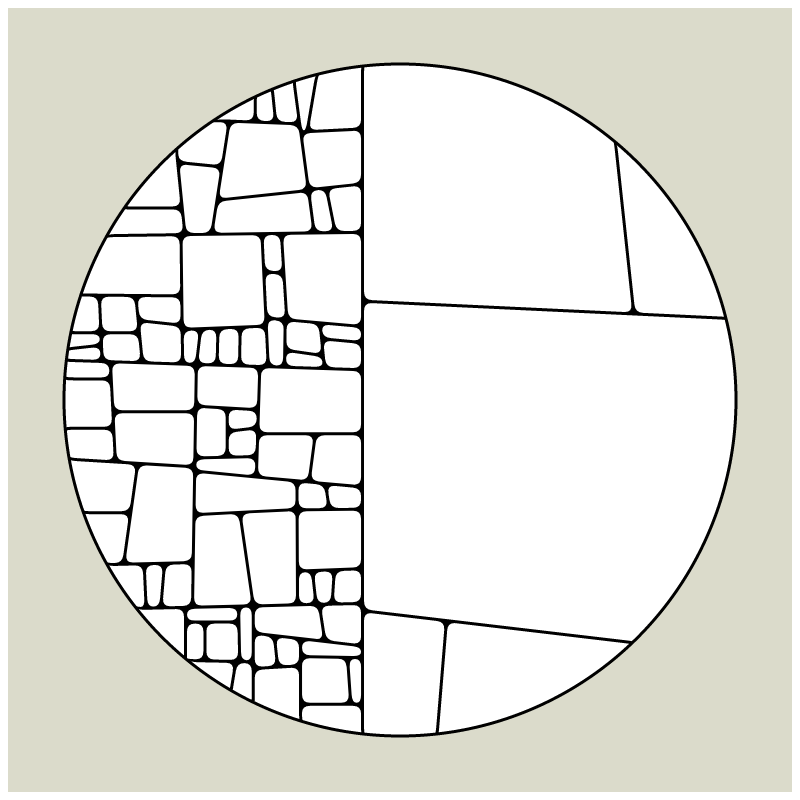
In my subdivision series I explored the many ways recursion can be applied to geometric shapes, starting with simple convex shapes and then expanding into non-convex or curved ones.

In "Redivision" I modernized one of my early codes and adapted it for the use with fx(hash) features.