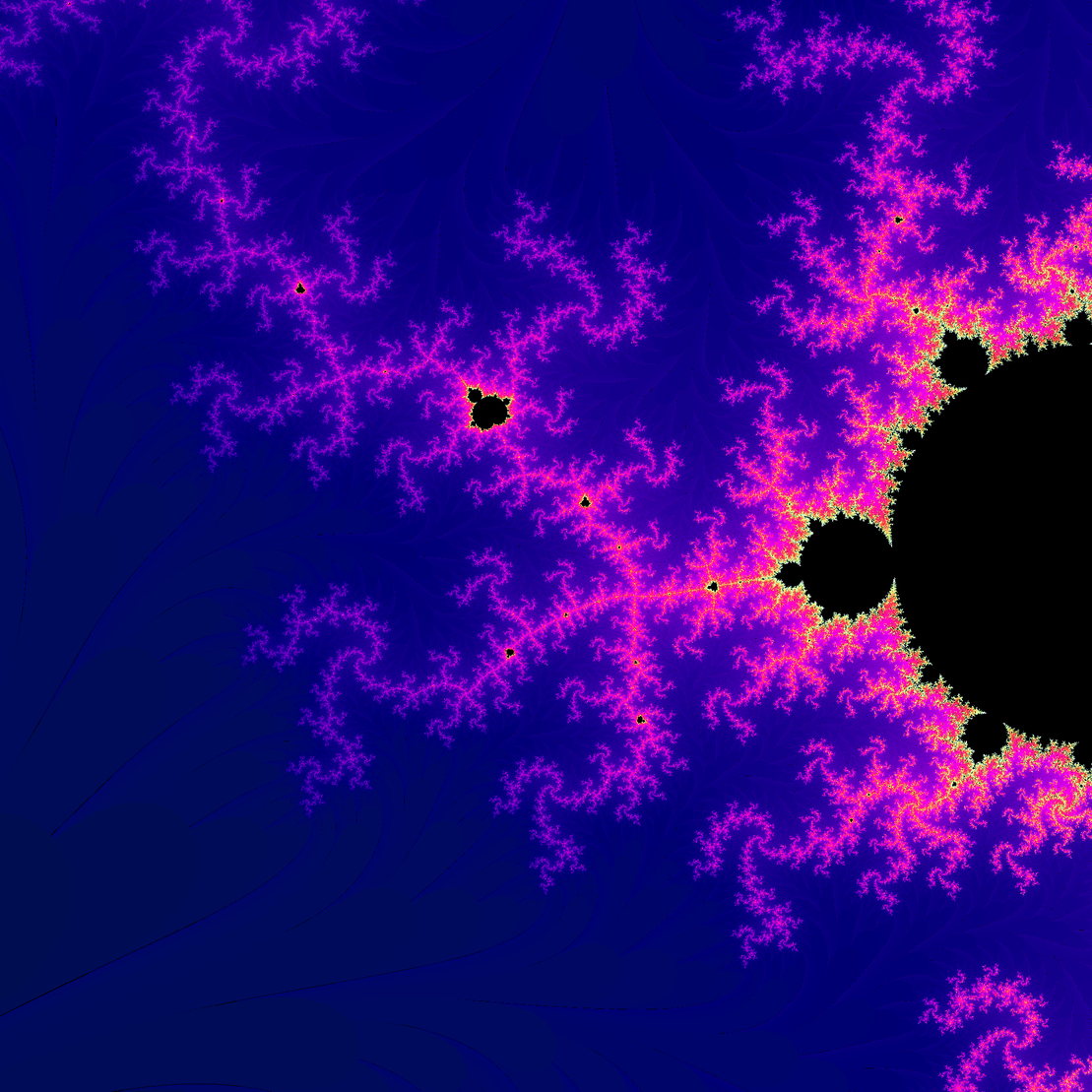
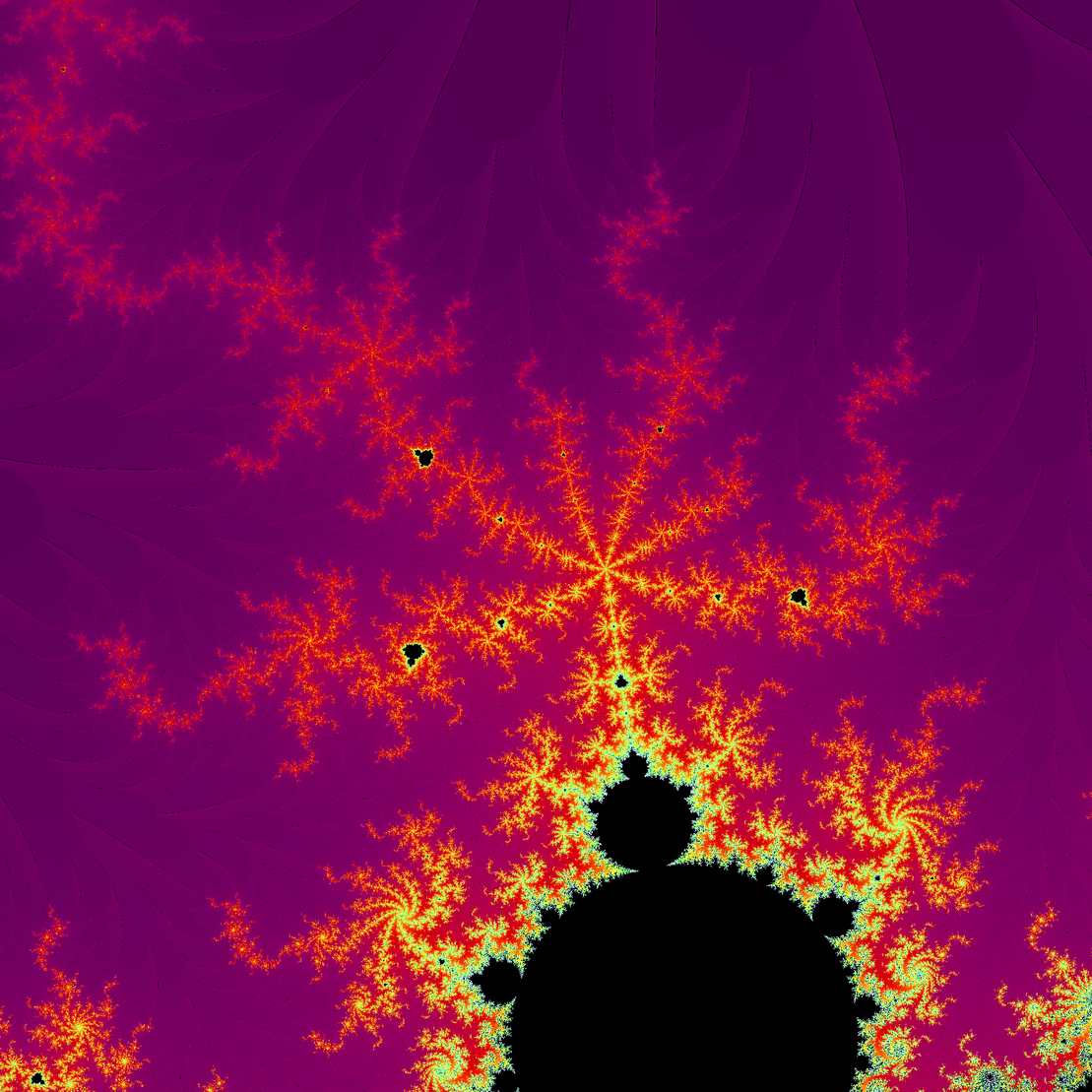
Mandelbrot is a fractal equation that has infinite amount of special locations. It is named after its founder Benoit B. Mandelbrot. Each point in fractal is calculated using equation z_{n+1} = z_n^2+c which is iterated until it diverges to infinity or not.

This algorithm searches mandelbrot equation for interesting location. These locations are such that are few iterations on borders and many iterations on the center of screen. After finding good basic location, locations around that are studied using local search. The best location is drawn.

This search uses hash for random locations and colors, and thus every hash yields unique result location. We cannot guarantee that 100% of the results give result in 300 seconds, but however, in tests, every hash got a result in one minute.

It takes around 30s to 1 minute to find a solution and draw it with proper cpu. Algorithm generates 2000x2000 pixel image of founded solution.

Coded using vanilla javascript.