by _pixelform_
Hanging Gardens
IPFS

6 July 2022•TEZOS•IPFS
An exercise in extending the well known and highly recognizable 1D elementary cellular automata.
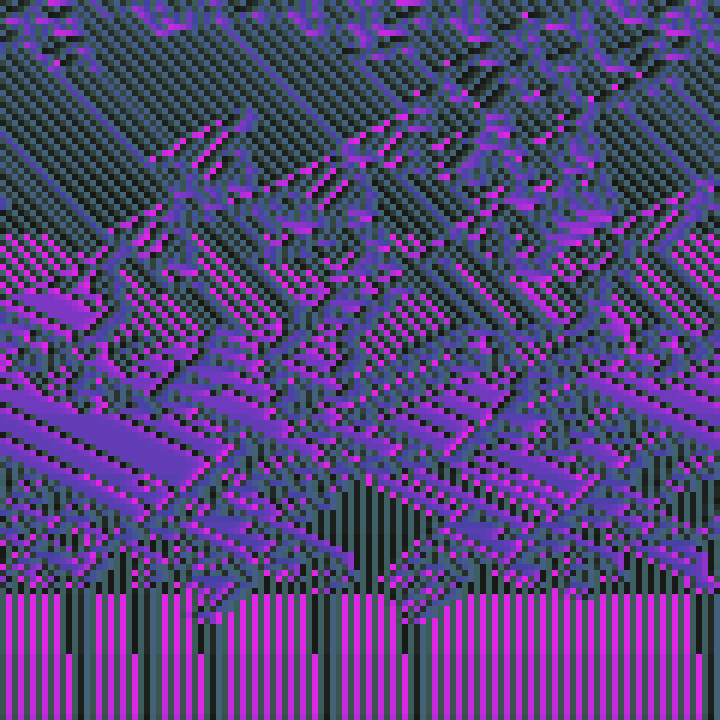
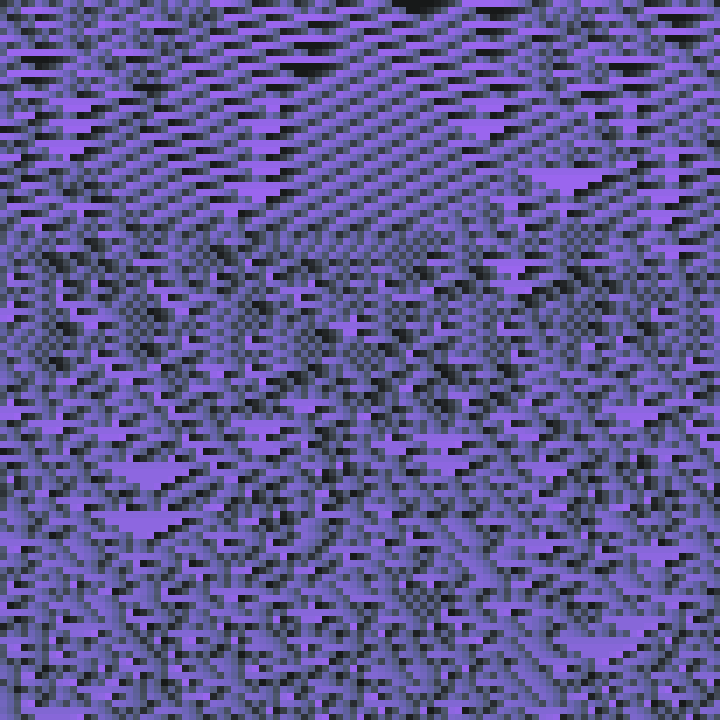
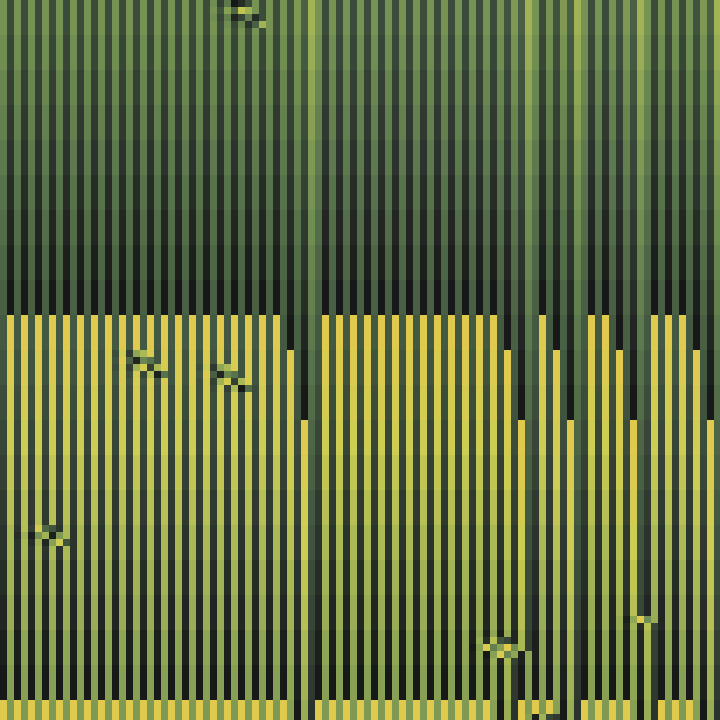
The 1D CA we're familiar with involve a row of cells. Each cell has 2 states: on or off. The future state of each cell is determined a rule set, which uses the current state of the cell in question and its neighbors, typically, 3 cells in total. The number of rules in this scenario is given by 2^(2^3) => 2^8 = 256.
Hanging Gardens explores much larger rule spaces, where 5-7 neighbors are considered in determining the future state of each cell. For a scenario where 5 neighbors are considered, the number of rules becomes quite large: 2^(2^5) => 2^32 = 4294967296 rules.
Since each cell's state is determined by its neighbors, it can be colorized according to the value of that state. In a system where there are 5 neighbors considered, the number of all possible neighbor states for a given cell is 2^5 = 32. The state is used as an index to choose a color from a pre-generated palette. This palette is a deterministically generated gradient starting with a hue of relatively high saturation and brightness, fading down to a different hue of low saturation and brightness. As each row is rendered out, the index is shifted over time to create a color cycling effect.
Static rules are no fun, and even dynamically changing rules can result in static outcomes, which may run that way indefinitely. To combat this, cells and rules will mutate over time at a rate established when the piece is initialized.
Controls:
SPACE - starts and stops the animation
1 - 1-bit black and white color
2 - greyscale color
3 - full color
The 1D CA we're familiar with involve a row of cells. Each cell has 2 states: on or off. The future state of each cell is determined a rule set, which uses the current state of the cell in question and its neighbors, typically, 3 cells in total. The number of rules in this scenario is given by 2^(2^3) => 2^8 = 256.
Hanging Gardens explores much larger rule spaces, where 5-7 neighbors are considered in determining the future state of each cell. For a scenario where 5 neighbors are considered, the number of rules becomes quite large: 2^(2^5) => 2^32 = 4294967296 rules.
Since each cell's state is determined by its neighbors, it can be colorized according to the value of that state. In a system where there are 5 neighbors considered, the number of all possible neighbor states for a given cell is 2^5 = 32. The state is used as an index to choose a color from a pre-generated palette. This palette is a deterministically generated gradient starting with a hue of relatively high saturation and brightness, fading down to a different hue of low saturation and brightness. As each row is rendered out, the index is shifted over time to create a color cycling effect.
Static rules are no fun, and even dynamically changing rules can result in static outcomes, which may run that way indefinitely. To combat this, cells and rules will mutate over time at a rate established when the piece is initialized.
Controls:
SPACE - starts and stops the animation
1 - 1-bit black and white color
2 - greyscale color
3 - full color
Work by Phillip David Stearns, grizzled electronic art veteran.
64 EDITIONS
•0 RESERVES
minted
64 / 64
fixed price
5.12 TEZ
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH