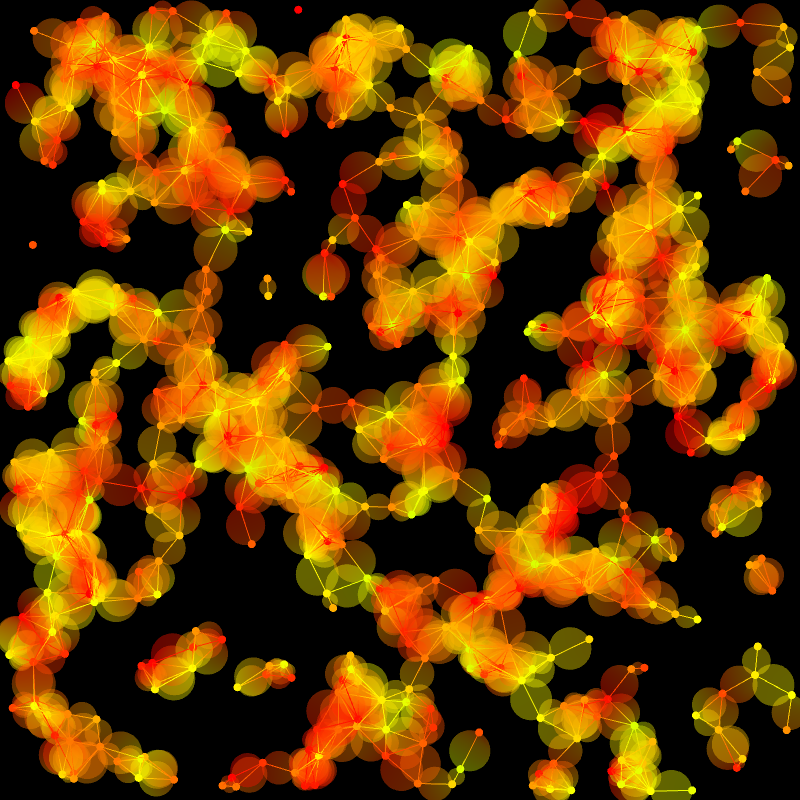
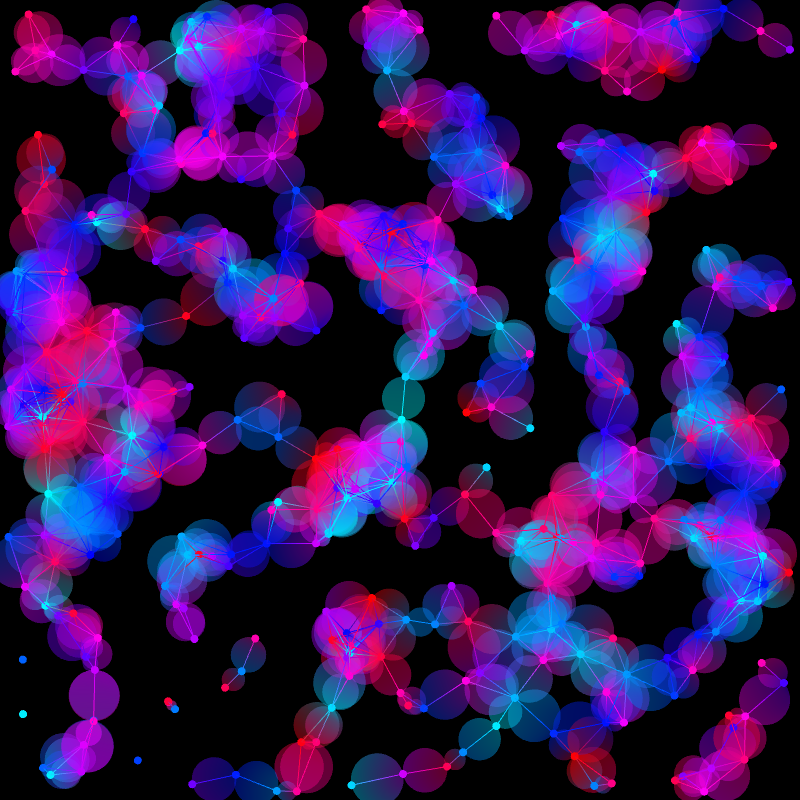
Gradient Graphs
IPFS

8 May 2022•TEZOS•IPFS
A Gabriel Graph is a special kind of graph in graph theory where an edge can only be formed between two nodes if the circle formed by those two nodes contains no other nodes in the graph. A Random Geometric Graph is a graph where an edge can only be formed between two nodes if they are less than a certain distance away from each other. In this project, I have created random Gabriel Graphs and Random Geometric Graphs, where the graphs have a random number of nodes and each node has a random position. Each node is assigned a color, and each edge is colored according to the two nodes at each end, with a gradient line and a gradient circle which slowly transitions from one color to the other. Users can interact with the project to remove the nodes, edge lines, or edge circles, choosing how they would like the graph to be displayed.
Made with p5.js
Press 'a' to toggle the edge circles on and off.
Press 's' to toggle the edge lines on and off.
Press 'd' to toggle the nodes on and off.
This code and its output are licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) License.
Made with p5.js
Press 'a' to toggle the edge circles on and off.
Press 's' to toggle the edge lines on and off.
Press 'd' to toggle the nodes on and off.
This code and its output are licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) License.
Software Engineer. Generative Artist. Adjunct Instructor at SMU's Center of Creative Computation.
100 EDITIONS
•0 RESERVES
minted
48 / 100
fixed price
1 TEZ
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH
Lorem ipsum project longer longer
0.00001 ETH