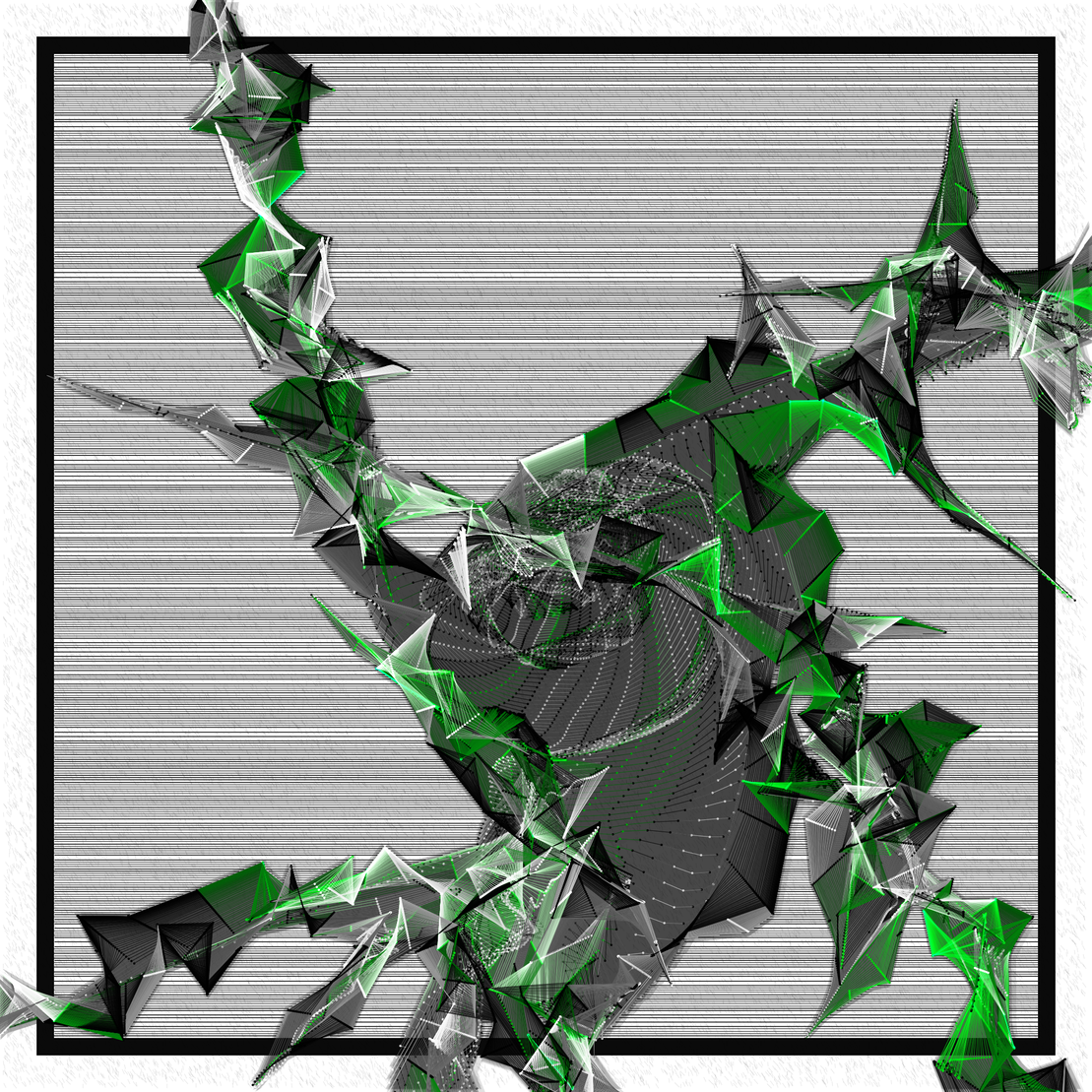
Chaotic growth is based on a modified version of the differential line algorithm by Anders Hoff [1]. This algorithm uses an attraction-repulsion-model to imitate growth on a connected set of nodes.

In this piece I explored an adaption of this algorithm attempting to visualize systems growing past their point of sustainability, creating new dynamics and eventually spiraling out of control. Some iterations may grow smoothly for some time but will quickly turn into a chaotic system of unsustainable growth. The smooth and organic shape of growth in the beginning is contrasted by the spikey, incoherent offshoots.


Created in Vanilla JS.

Controls:
S - Save image
Space - Pause/Unpause


Best viewed in Chrome. Different browsers may produce slightly different outputs.

[1] https://inconvergent.net/generative/differential-line/