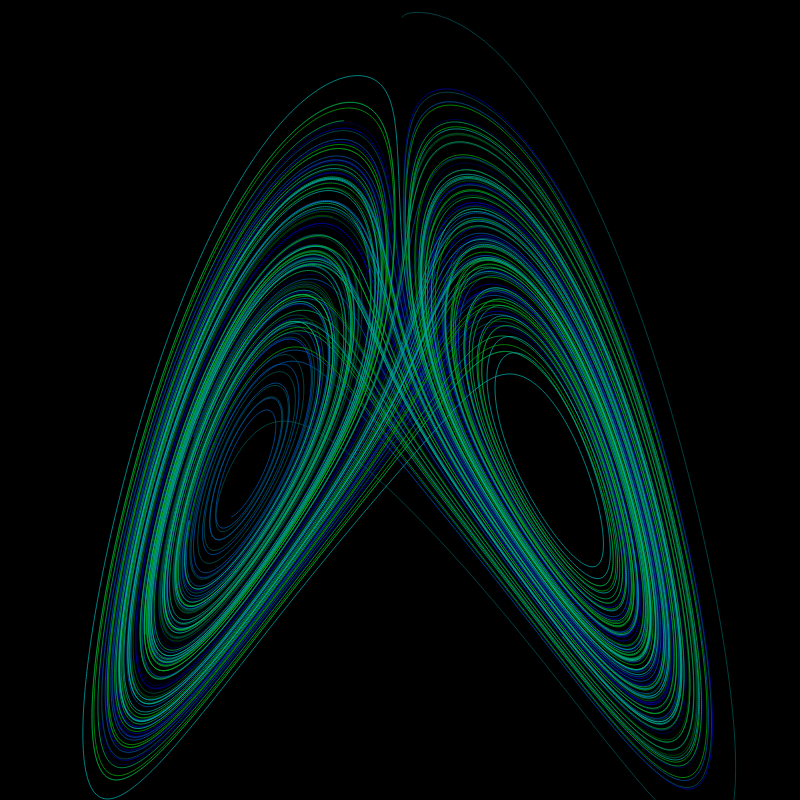
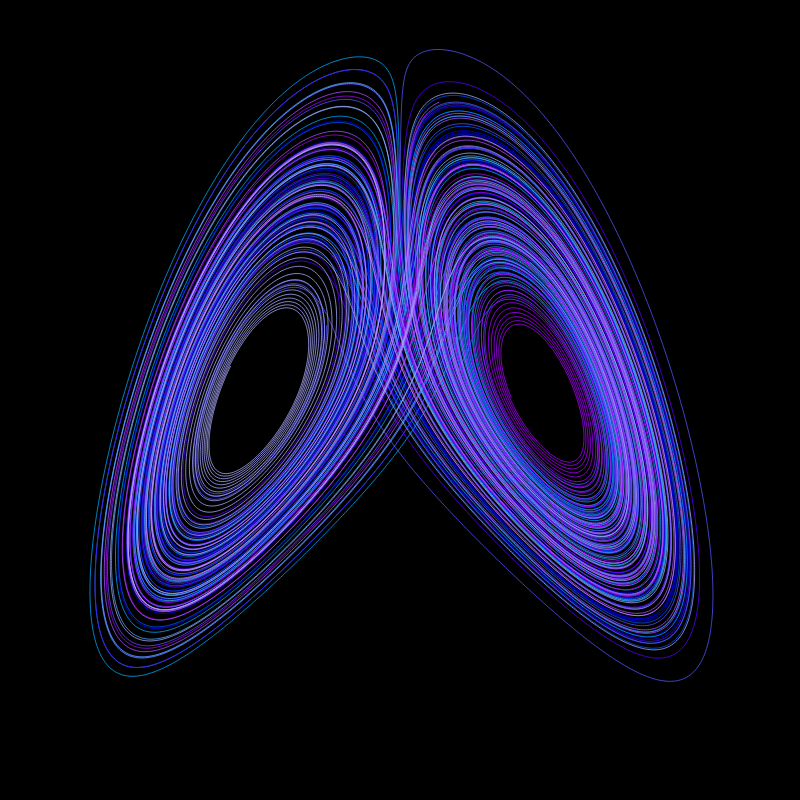
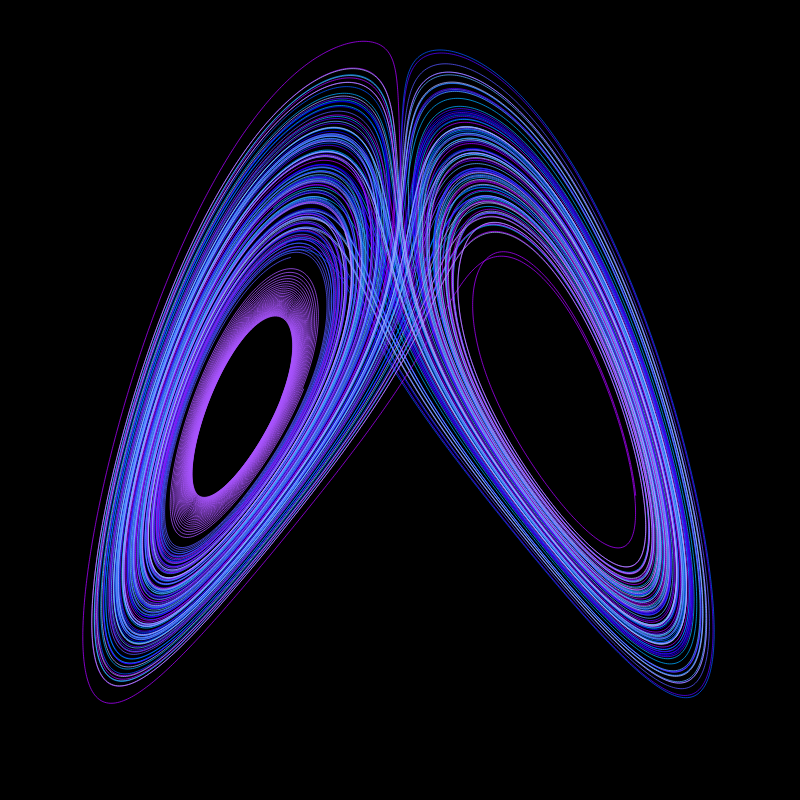
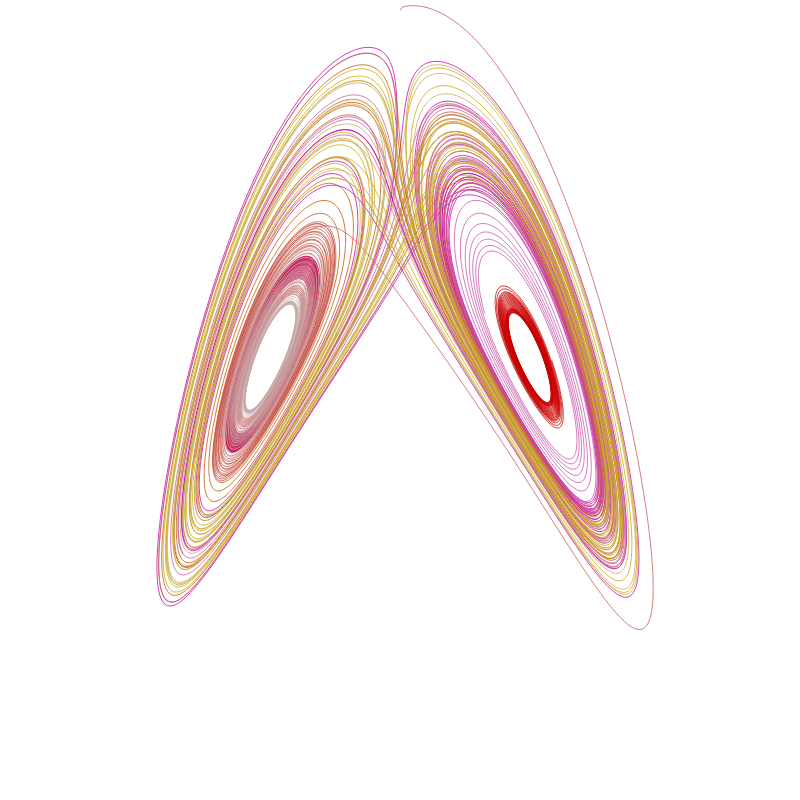
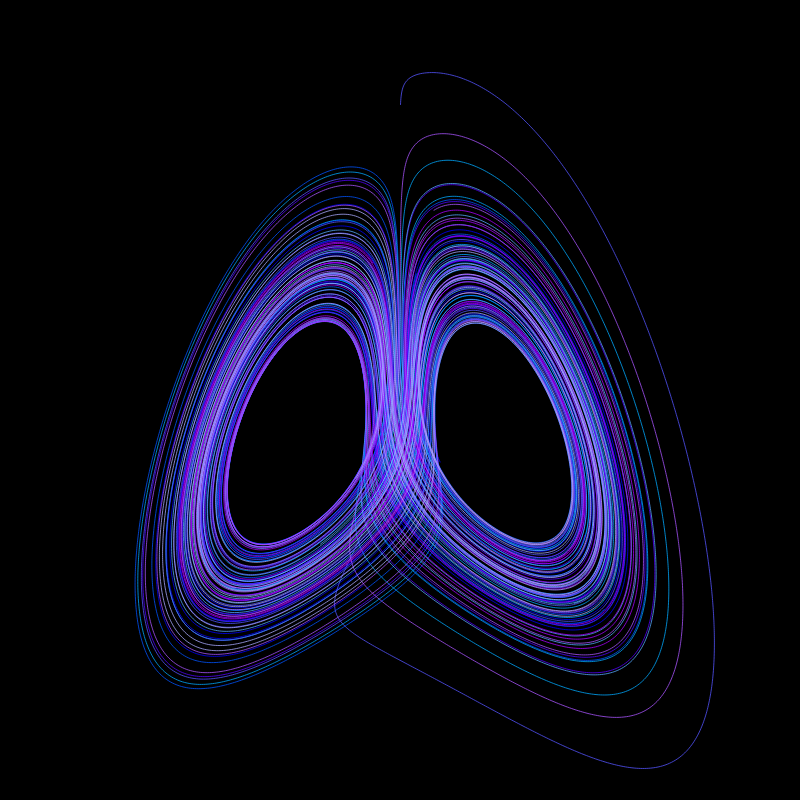
A Lorenz attractor. Each varies in parameters so that every one has a unique shape. Chance for different colors and rotation speed. Built from scratch. Implements Runge-Kutta-Fehlberg method (RK45) for solving ordinary differential equations. Rendering canvas only. Isometric projection.

Controls:
* Click to drop in sample tracing points. Watch them fly around
* Space to pause/play rotation
* Drag to rotate
* Arrows or Shift + Drag to pan
* 'r' to reset view
* 'c' to clear points
* Scroll or '+' '-' to zoom in and out