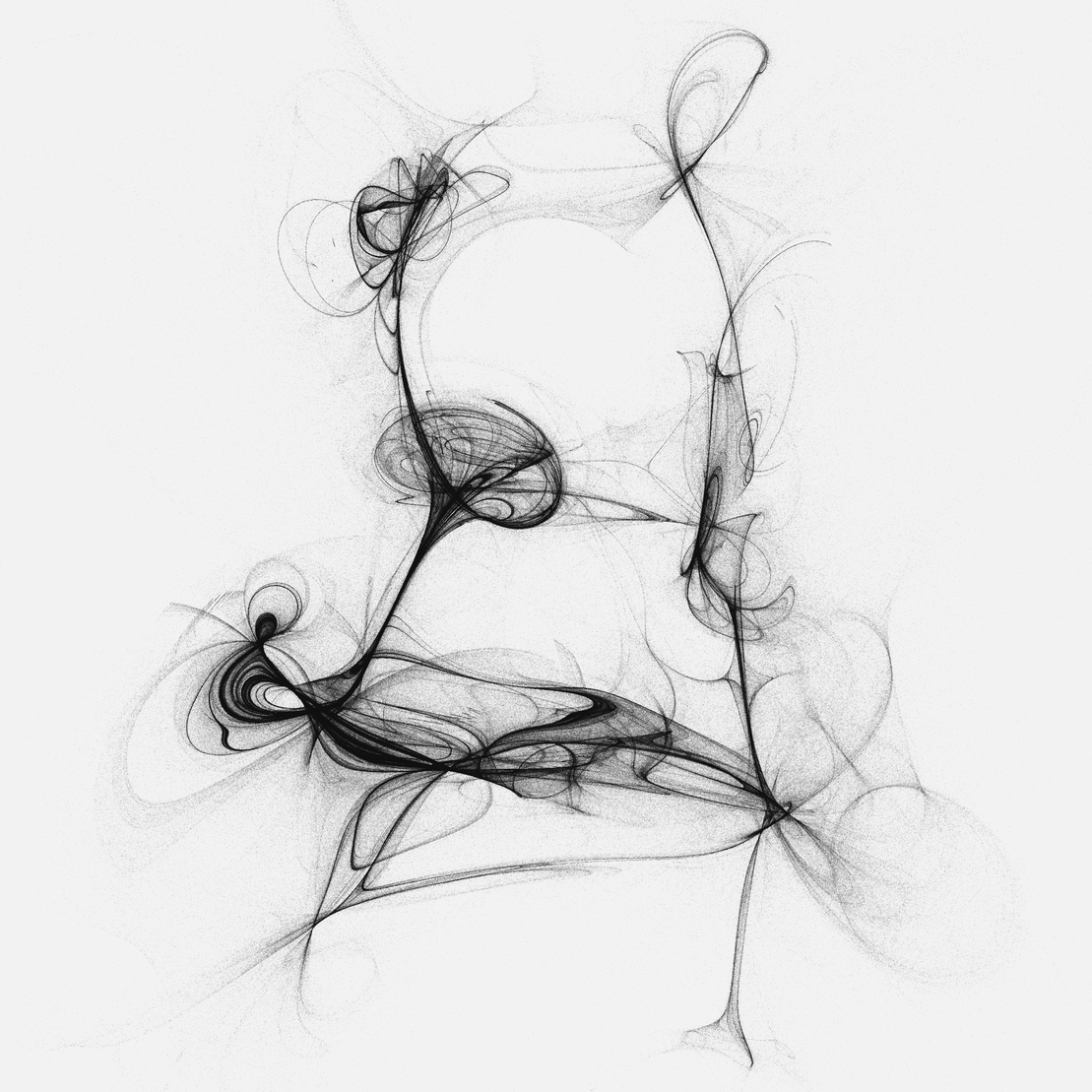
Si-operator
written by HAL09999
All known life on Earth is made of CHONPS
That’s it: carbon, hydrogen, oxygen, nitrogen, phosphorus and sulfur account for 99% of the mass of all what are considered as living things.
Carbon (C), thanks to its high affinity for the other elements and its ability to form complex molecules, acts as a backbone for all molecular structures that constitutes living matter. In fact, the only known forms of life on Earth are carbon-based.
However, carbon only makes up approximately 0.03% of the Earth’s crust by mass. This is relatively small compared to silicon (Si) which comprises more than one thousand times that amount, accounting for approximately 28% of the mass of all available elements on Earth’s surface.
Silicon could be a good replacement candidate as it shares many chemical similarities with carbon. It can form as many covalent bonds and participate too in the creation of complex molecules. There are many structures mixing carbon and silicon and they are known as organosilicon compounds.
Yet, to date, no silicon-based lifeforms have been discovered.
Silicon-based memories
Viruses, fungi, algae, humans, birds and crocodiles, but not only, have the vast majority of their structural information encoded in long DNA molecules curled up inside cells. DNA as well is structured by repetitive sequences of carbon-based motives.
This brings to draw a simple parallel between computer memory and DNA molecules used as a data storage medium.
DNA encodes information using four basic units called nucleotides : Adenine—Cytosine—Guanine—Thymine, where most of current era computing uses a binary system 0—1. In fact, there are already some kinds of computer data storage that uses DNA as a medium.
While there are many hypothetical alternative biochemistry theories, one of the most famous silicon-based lifeform appears in science-fiction, the well-known Alien movie evolves around the existence of an alien lifeform called the xenomorph.
We could also cite this experiment, using a molecular machinery extracted from a bacteria as a catalyst for organosilicon chemistry. Or the less famous Horta monster from Star Trek.
All these researches about silicon-based lifeforms are very inspiring for science-fiction, but there is a field where the importance of silicon in the emergence of autonomous processes may be underestimated...
The uncanny valley of numbers
Being scared by strangeness is a very natural feeling. Strangeness arises when what we experience is similar to what we know, but a little different. Think of the Frankenstein complex or the concept of uncanny valley in robotics.
« A Theory of General Instability » was partly inspired by the feeling experienced when thinking about the probable emergence of an Artificial General Intelligence and the relations between humans an their past and present knowledge, as well as the infinite void of what's left as the unknown.
Coexisting with something that will obviously be more clever than us, or let's say "more computationally capable", can bring some questions like "What are the boundaries of what we can understand ?", "How knowledge is produced and transformed ?", and how humans will manage communication with a more powerful general intelligence. One that could probably incorporate all knowledge produced to date in a single entity, while synthesizing concepts with a bandwidth that is hardly imaginable for current humans.
Today, the vast majority of all algorithms running on Earth (and even in outer space as humans already launched a large quantity of computers there) are computations made on silicon-based devices. Even the recent advances in computer neural network technologies, some evolved forms of machine learning (a practical computerized application of statistics) are still algorithms, and still work thanks to the nanoscale structures engraved in the silicon that make "chips" : processors and memories.
Code as law, number as origin
Did this output existed before ?
« Si-operator » uses minter’s wallet address as a seed for all its pseudo-random operations. Each wallet address have access to 20 specimens and much more variations thanks to the other parameters.
The pseudo-random number generator (PRNG) being seeded only by minter’s wallet address, we can therefore imagine that the device's outputs only depends on :
- an opaque box — the algorithms
- a number seed — the minter’s wallet address
- three choices — specimen, waveguide system, and q-phase value
While the algorithms are well defined, they are able to create an infinity of shapes and outputs, given an infinity of inputs. At the moment of creating the generator there is a very big number of possible outputs, so big that in fact it’s totally impossible to predict what will be the exact generated shapes. « Si-operator » being a deterministic generator, each potential seed can be directly linked to a finite set of 40 shapes and approximately a hundred shades of contrast.
By the action of the minter, the system evolves from a superposition of all possible states to a unique output depending solely on minter’s wallet address and its choices.
A curious question to ask oneself is whether this output existed before, and if it is the case, where ?
Observation
In fact, this question is kinda wrong as it is paradoxical : we only know if something exists if there is a way to observe it.
Another question, which answer may, at first, seem more obvious is how do we know if there is something here ?
Imagine an empty room then add a human, an elephant and a spotlight. Human wonders: is there something else in the room ?
We might be tempted to think that the answer is immediate: if there is an elephant in the room then the human must see it… but we need to be more precise. If there is a spotlight orientated so the elephant is lit enough, if the elephant is close enough to the experimenter, the human’s eyes must receive some of the light that the elephant reflects and therefore conclude that there is something else in the room.
The light emitted and reflected acted as a signal, and the eye of the human as a sensor, the conclusion of presence being left to the human experimenter.
Using a small 20W lamp should be enough to at least see that there is a big elephant. If the elephant is patient and bears the spotlight, nothing serious should happen to the human. Let’s call this measurement “non-destructive” : after the experiment, the elephant and the experimenter should be almost in the same state than before the experiment, except that now they both know there is something else in the room. But if you are familiar with elephant psychology it is already possible to sense that this kind of experiment can have a totally different outcome.
Now imagine using a 300-meter-high ruler weighing 1000 tons to measure the height of a human: even if the giant experimenter is very delicate, there is a quite high probability for the human to be squished inadvertently.
There is an evident relation between the scale of an experiment and the ease of making a non-destructive measurement. In fact, at scales where the wavelength of light appears as a giant, atoms feel like the small human.
From these simple thought experiments it is easy to understand how the observation can affect the subject.
It's a long read, I thought you would explain operators ?!
OK, ok... In quantum physics, measuring things is easier to do in theory than in practice. Experimentally, it consists of wiring lots of devices to low-noise sources and amplifiers and hoping for the best. But, follwing quantum physics theories, all kinds of observations you can imagine can simply be described by operators.
Quantum physics describes all the observable data about something as a “state”, and all the probabilities for the object to be in a specific state by wave functions. For example, as physicists like particle very much, the state of a particle can be a description of its whole energy, speed and maybe position.
That’s the usual for the material world : we need to know where are things, how fast they move, and in which direction (think about the elephant or the giant ruler).
So, in the quantum description of nature, we can describe all the needed data about a particle by writing its wave function, usually symbolized like this
∣Ψ(t)⟩This symbolic representation holds all the probabilities for the particle to be in a particular state at a particular instant in time. But, how do we go from this, to knowing where it is ?
Quantum physics describe the operation of extracting an observable (the position) from a system with the help of a mathematical tool called an “operator”. As we’re interested in knowing the position of the particle, let’s apply a position operator to its wave function :
⟨r∣ψ(t)⟩=ϕ(r,t)For those who like the mathematical scriptures, the kind of elegant notation seen on the left is called “bra-ket” and is heavily inspired from vector calculus. The right side of this equation is a “probability amplitude”: it holds the probabilistic description of the position of the particle at any given time t. Meaning that for any instant in time this equation will return a probability for the particle to be at a certain location in space.
That probabilistic description is what is currently known as the most accurate theoretical description of physical reality.
But, to be accurate, applying an operator doesn’t give the exact position of the particle, it only gives probabilities. To determine the exact location of the particle we need to probe the space with something and wait for a signal back. That's why, for the experimental quantum physicist, most measurement are said destructive : at very small scales light is something very big that will for sure disturb the observed system, like being pursued by a 1000 tons ruler could feel disturbing.
Experience
project name project name project name
This is a fully animated generator, click "run" to observe the animation. Use wheel to change the observation scale. Drag with right click to observe a different area. This live animation is designed to be experienced fullscreen on a 16/9 screen at least full HD, and needs a recent (>2015) graphic card (GPU) to run smoothly at its cruise speed of 60FPS.
Click "project" then "open" to see the live version in full window, or click HERE. Click "params" to open a live view on the choices available for the observation of the Si-operator, or click HERE.
Observation parameters
All available explanation about parameters are displayed in the "params" view.
I hope you enjoy this experience and its outcomes ! You can contact me on fxhash discord or Twitter DM for any question or request.
[ Follow @HAL09999 on Twitter / @hal09999 on instagram / Follow hal09999.tez on objkt ]