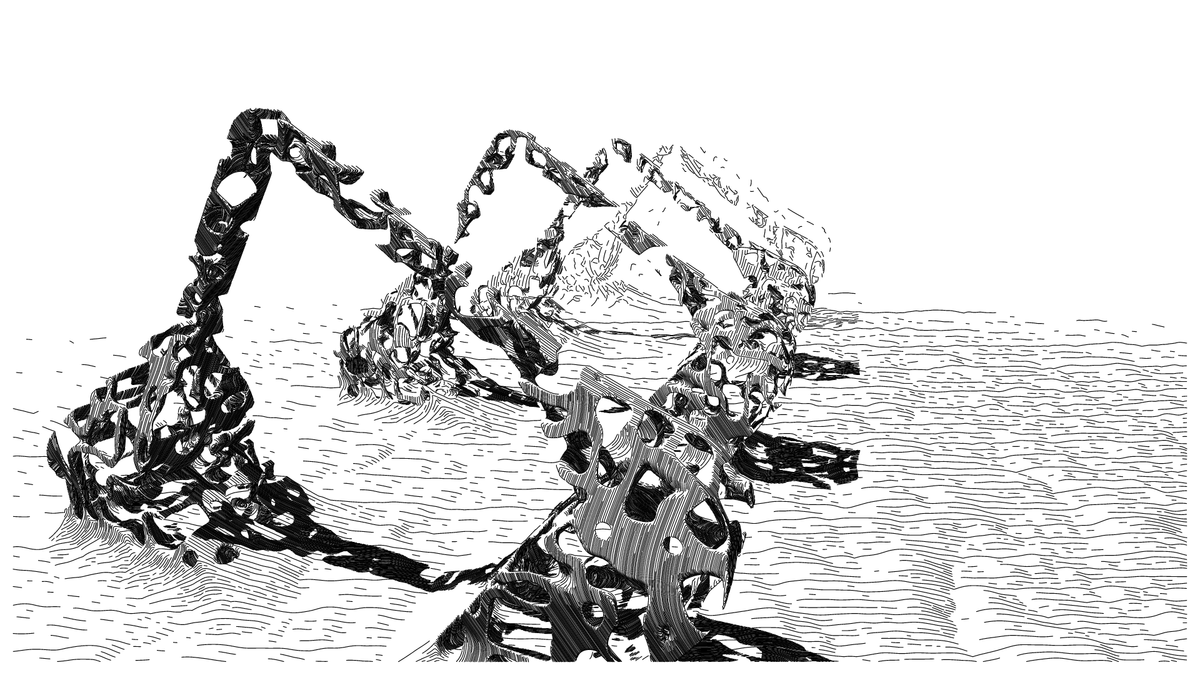
Revolving, twisting and transforming SDFs!
written by antiforma
One of the highlights of late on (fx)hash has definitely been the Universal Rayhatcher project by Piter Pasma
It brings the (fx)params idea to the extreme by allowing the minter not only to customize the work, but really to specify the shapes that the rayhatcher algorithm should draw on the screen, practically giving the freedom to create almost anything.
project name project name project name
Many artists have been creating incredible works by crafting what are basically mathemathical formulas, more precisely an idiom of SDF - signed distance functions.
Once you’ve seen what have been made with URH, you’ll probably want to try yourself, specially if you are not afraid of math :). Some articles have been published that really help to get started.
- The first by Ethspresso, explaining the basics of URH and SDFs and showing most of the ideas and building blocks you’d want to use
- Another by clauswilke deconstructing his truchet tiling SDF and giving an in depth view of the process required to build a more complex piece.
- Last but not least, another one by clauswilke with a deep dive on how to build the SDF for an UFO flying over a landscape
This here is my humble contribution, and the recount of some of my attempts to understand the gist of SDFs and how to go beyond the basic shapes.
I have to warn you that I’m a beginner myself, so I’m also looking for suggestions on how to correct what I wrote and how to better implement the ideas presented here.
The main reference for URH is the official documentation page, and anyone can use the live development environment to try out the formulas.
Orienting oneself
The first issue I had when trying to make something with URH, was that the orientation and the light source of the scene is obtained from a seed calculated from your tz address plus the title field of the params, and cannot be really finely controlled.
At first I had trouble understanding what direction was up or down and where the axes were oriented, if you ever tried to take an SDF from the minted tokens and use it in the development environment, with your tz address you’ll have seen that the results are different from what was minted.
What may help is to draw the axes and understand which direct is positive and which is negavite.
_a = U(
L(x,y,0)-0.3,
L(0,y,z)-0.3,
L(x,0,z)-0.3,
bx3(x+20,y,z,1),
L(x,y+20,z)-1.5,
don(x,y,z+20, 1.5, 0.5),
);
_a
_a draws the axes with: a cube on the positive side of the x axis, a sphere on the positive side of the y axis, a donut on the positive side of the z axis.
If we need to draw the axes together with any other shapes, just draw their union:
U( _a, bx3(x,y,z,6,2,3))
Revolving
One surprising realization was that we can draw many shapes by defining a 2-dimensional shape and moving it along another 2-dimentional path. An example of this is revolving a circle around another circle to obtain a donut.
This is the SDF for a donut of inner radius a and size b:
L(L(x,y)-a,z)-b
It may be read as finding the points at distance `b` from the coordinate `z` and any point on the circle of radius `a` on the `xy` plane. The inner SDF: `L(x,y)-a` is wrapping the space around the cylinder of radius `a` and the effect if that of revolving the `b` radius circle around the `a` radius circle.
Whenever we have a 2-d SDF on the `xz` plane and replace the `x` coordinate with the 2-d circle on the `xy` plane we obtain the shape defined by revolving the `xz` shape around the `y` axis.
Notice how the sphere could also be drawn by collapsing the inner circle to `a` radius 0:
L(L(x,y),z)-b
for instance, if we take the box SDF (`bx2`), we may build a wheel:
bx2(L(x,y)-a,z,b)
An angle can be defined as:
B(x)
It's easy to get caught playing with different functions. Some of them will produce interesting shapes, other will get artifacts or not much. It is really useful to draw a function (even if just 1-d) to see what shape it creates, a nice tool to do so is
. For instance, the angle above is
revolving the angle around the center gets us an infinte cone:
B(L(x,y))+z
Intersecating with a plane we can obtain a finite cone:
G(B(L(x,y))+z,-z-a)
from the rhombus (or infinite prism) B(x)+B(y)-10 we can obtain a double cone:
B(L(x,y)-30)+B(z)-10
revolving a cosine (or sine) around a circle gets us a concentric waves:
cos(L(x,y)-30)+z
A circle is not the only path you can try to use!
The hyperbole is the locus of the points of the plane for which the difference between their distance from two fixe poins is a constant. Writing this in the URH SDF idiom, we'd have:
B(L(x-a,y)-L(x+a,y))-b
This describes the hyperbole with foci in (-a,0), (a,0) and distance constant b. You can define an SDF plugging that in the circle SDF:
The parabola is the set of points for which the distance from a focus point is the constant with respect to the height of the point (distance from the axis): B(L(x,y)-y)-a. Try to plug it instead of the hyperbole SDF in the above formula!
Using the same technique we can draw a frame by moving a square along another square:
bx2(bx2(x,y,10), z, 2)
or moving a circle along a sinus/cosine
L(cos(x)*10-y*6,z)-2
or even a circle along a triangular path...
L(TR(x)*4-y*2,z)-2
Twisting
Above I wrote that we can think of the revolving operation as actually transforming the coordinates, and we can use this idea to do much more!
One example is that we can deform the coordinates by wrapping them around an axis.
Define this function:
tw=( a, b, c, t1, t2)=>(
e = cos(t1*a),
f = sin(t2*a),
[a, D([b,c],[e,-f]), D([b,c],[f,e])]
),
tw bends an SDF around the first coordinate `a`, by an amount given by `t1` (along axis `b`) and `t2` (along axis `c`).
[x,z,y]=tw(x,z,y,0.05,0.05),
don(x,y,z,30,10)
[x,y,z]=tw(x,y,z,0.02,0.02),
bx3(x,y,z,10,20,5)
if we use a box wide enough we can get a bent strip
[x,y,z]=tw(x,y,z,0.02, 0.02),
bx3(x,y,z,100,10,1)
not only this but by repeating (with modulo operation), we can get a strip of rotating boxes:
[x,y,z]=tw(x,y,z,0.02, 0.02),
bx3(mod(x,20)-10,y,z,2,10,5)
or even more comples figures, like an helix:
[x,y,z]=tw(x,y,z,0.05,0.05),
L(bx3(mod(x,40)-20,y,1,20,20),z)-4
or this:
[x,y,z]=tw(x,y,z,0.05,0.05),
G(L(bx2(mod(x,20)-10,y,20,40),z)-4,y)
You may have noticed that in the last example what I did looks like intersecting a twisting double cylinder with the xz plane, which would return a positive value for the SDF only for positive values of the y coordinate.
It may be surprising that it does not actually cut the scene on the xz plane but it shows only one of the twisting cylinders (I know I was suprised at first). What really happens is that the twisting function transforms the coordinates, so the cut plane is actually bent together with the rest of the figure!
What next?
Universal Rayhatcher and SDFs can be intimidating and look alien somehow, but it's really easy to go on the development environment and try it out. Start with basic shapes and apply some of the ideas outlined in the documentation and articles that are popping up, you'll get surprised with what you'll be able to create with it!
P.S. this is the code for the first image above
tw=( a, b, c, t1, t2)=>(
e = cos(t1*a),
f = sin(t2*a),
[a, D([b,c],[e,-f]), D([b,c],[f,e])]
);
[xr,zr,yr]=tw(x,z,y,0.05,0.05),
U(
B(L(x,z)-40)+B(y)-10,
cos(L(x,z)-30)+y+20,
bx2(bx2(mod(xr,20)-10,zr,15), yr, 2),
G(bx2(bx2(x,z,15), mod(yr,20)-10, 2), -yr+20)
)